Gleichungen lösen: Regeln einfach erklärt + Beispiele

Kapitel:

1. Was sind Gleichungen?
2. Einfache Gleichungen lösen
3. So löst du lineare Gleichungen
4. Quadratische Gleichung lösen: Formel & Beispiele 
5. Lösung von Bruchgleichungen: Variable im Zähler oder Nenner
6. Polynome in Gleichungen lösen

Gleichungen sind ein wichtiger Bestandteil der Mathematik. 🧮 Für die einen sind sie ein Thema 🙋 der Leidenschaft, für andere dagegen ein Thema, das Leiden schafft.  Das muss nicht sein, denn Gleichungen lassen sich lösen! Wir erklären dir, was Gleichungen sind und welche Arten es gibt. Und natürlich das Wichtigste: Lerne Lösungswege 💡 für gängige Gleichungen. Fangen wir gleich damit an! 😎

Was sind Gleichungen?

Gleichungen bestehen aus zwei Teilen und einem Gleichzeichen (=) in der Mitte. Die zwei Teile nennt man auch Terme. Es gibt also eine linke Seite und eine rechte Seite der Gleichung und das mathematische Gleichheitszeichen (=), das die zwei Terme verbindet. Also: Term links = Term rechts. Zum Beispiel: 7 = 7.

Aber viele Terme sehen auf den ersten Blick nicht gleich aus. Es können beispielsweise zwei Mathe-Aufgaben links und rechts stehen. Du musst die Aufgabe zuerst lösen um zu sehen, ob dieselbe Zahl herauskommt. Zum Beispiel: 2 + 2 = 1 + 3.

Gleichungen können entweder wahr oder falsch sein. 

Damit eine Gleichung wahr ist, müssen die beiden Seiten gleich sein. Also: Der Term, der links vom Gleichzeichen steht, muss dem Term rechts vom Gleichzeichen ensprechen. Zum Beispiel: 3 = 3. Oder: 4 + 1 = 3 + 2. Damit ist die Aussage der Gleichung wahr. 😀 

Entsprechen sich die Zahlen nicht, ist die Aussage der Gleichung falsch. ☹️ Zum Beispiel: 2 + 2 = 1 + 2.

Wenn du einen Buchstaben in einer Gleichung siehst, dann ist das kein Tippfehler von deinem Mathebuch, sondern eine Gleichung mit Variablen. Zum Beispiel: 2 + x = 6. Eine Variable kann für irgendeine Zahl stehen.

Gleichungen können zwei Terme auch mit einem anderen Zeichen verbinden. Statt dem = steht dann zum Beispiel > (größer), < (kleiner), (kleiner gleich), (größer gleich) oder (ungleich). Das nennt man dann Ungleichung. Mit der Ungleichung zeigst du, dass ein Term größer oder kleiner ist, als der andere. Also: Term links > Term rechts. Zum Beispiel: 2 + 3 > 4. (Gesprochen: zwei plus drei ist größer als vier.)

Nochmal zusammengefasst:

• 2 + 5 = 7 ist eine wahre Aussage
• 2 + 5 = 10 ist eine falsche Aussage
• 2 + x = 10 ist eine Aussageform mit Variable
• 3 10 und 10 >3 sind Ungleichungen

Welche Gleichungen gibt es?

Wahrscheinlich hast du in der Mathematik gelernt, dass es unterschiedliche Gleichungen gibt. Die Terme beziehungsweise wie diese formuliert sind, bestimmen die Gleichungsarten.

• Lineare Gleichungen: x + 4 = 10 

Lineare Gleichungen enthalten Unbekannte nur in der ersten Potenz.

• Quadratische Gleichungen: x² = 9

Quadratische Gleichungen können Variablen der ersten bis zur zweiten Potenz enthalten.

• Potenzgleichungen: xⁿ = b

Die Unbekannte in Potenzgleichungen kommt als Basis der Potenz vor, welche höher als 2 sein kann.

• Bruchgleichungen:

Hier taucht eine Variable im Nenner eines Bruches auf.

Wozu sind Gleichungen nützlich?

Komplizierte Gleichungen verbinden die allermeisten nur mit dem Mathematikunterricht und komplizierten Textaufgaben 🚉 oder Schaubildern. 📈 Gleichungen sind aber immer dann hilfreich, wenn ein Wert gesucht wird und wir eventuell ein paar Annahmen treffen müssen, beispielsweise über unbekannte Variablen. 🔍

In den Naturwissenschaften 🧑‍🔬 und der reinen Mathematik sind Gleichungen unerlässlich. Im Alltag ist jeder Einkaufszettel 📜 mit einer Addition deiner Ausgaben 🛒 eine Gleichung, und wenn du dich fragst, wieviel Geld 💰 du übrig hast oder noch ausgeben kannst, löst du ebenfalls eine Gleichung.

Keine Lust auf Mathe muss übrigens nicht immer ein Anzeichen für Rechenschwäche sein, aber dennoch ist es hilfreich, die Symptome von Dyskalkulie zu kennen, um diese auszuschließen oder zu behandeln. 

Einfache Gleichungen lösen

Einfache Gleichungen lassen sich entsprechend auch recht einfach lösen. Sie haben eine oder wenige Unbekannte. 🕵️‍♀️ Für gewöhnlich ist eine Umstellung erforderlich, um auf die Lösung zu kommen.

• 10 + x = 99
• x + 3 = 2
• 25 - x = 17

Das Umstellen von Gleichungen erlaubt dir, die Terme auf beiden Seiten anders auszudrücken, solange die Gleichung äquivalent (gleichwertig) bleibt und ihre Aussage nicht verändert. Deswegen spricht man auch von der Äquivalenzumformung: Die Ausdrücke vor und nach der Umformung sind gleich. Bei dieser Umformung veränderst du beide Seiten, etwa mit den vier Grundrechenarten: Addition, Subtraktion, Multiplikation und Division. ➕➖✖️➗

Durch die Äquivalenzumformung kannst du schließlich Unbekannte so isolieren, dass du auf die Lösung kommst. 🤔

10 + x = 99 | -10

10 + x - 10 = 99 - 10

x = 89

Die Lösungsmenge L =89 gibt alle möglichen Lösungen für die Unbekannte an, für welche die Gleichung wahr ist, denn eine Gleichung kann auch für mehr als einen Wert wahr sein.

Übrigens: Unsere Nachhilfelehrer helfen dir gerne bei deinen individuellen Lernzielen weiter. Probiere es gerne aus und fordere jetzt eine gratis Nachhilfestunde an. Klicke dafür einfach auf den Button unten:

So löst du lineare Gleichungen

Lineare Gleichungen weisen faktorierte Unbekannte auf. Vor der Variablen steht also ein Faktor. Das Lösen erfordert die Division durch diesen Faktor, um die Unbekannte ermitteln zu können. 🧑‍🏫

• 5x + 5 = 25
• 2x + 7 = 21
• 100 - 4x = 0

Kommt in der linearen Gleichung eine Klammer 🗜️ vor, musst du diese zuerst auflösen, indem du die Klammer entsprechend den Regeln ausrechnest:

Wie gehen Essen und Mathe zusammen? Wir haben Tipps, wie Kinder mit Kochen und Mahlzeiten Mathematik lernen können! Du verstehst nur Bahnhof? Keine Sorge, unsere Mathe Nachhilfelehrer erklären dir alles Schritt für Schritt bei einer kostenlosen Nachhilfestunde.

Quadratische Gleichung lösen: Formel & Beispiele 

Quadratische Gleichungen enthalten eine Unbekannte im Quadrat, also eine Variable mit Zweierpotenz.

• 5x² +3x=54
• x²=64

Um eine quadratische Gleichung zu lösen, suchst du die Nullstelle, also die Lösungsmenge, für welche die Gleichung Null ergibt. Dazu formst du die Gleichung zunächst um, sodass auf der rechten Seite Null steht.

5x²+3x=54 | -54

5x²+3x-54=0

Jetzt hast du eine klassische quadratische Gleichung mit den drei Koeffizienten a, b, c und x als Unbekannte. In unserem Beispiel oben: a=5, b=3, c=-54 Eine quadratische Gleichung kannst du mit der PQ-Formel lösen. Lehrer und Lehrbücher der Mathematik 🧑‍🎓 nennen diese Formel häufig "Mitternachtsformel". 🌃 Warum? Wenn du im Mitternacht geweckt wirst, solltest du diese Formel quasi im Schlaf auswendig können! 🌙

Die allgemeine Form der quadratischen Gleichung ist:

ax²+bx+c=0

ax² heißt auch quadratisches Glied, bx lineares Glied und c konstantes Glied. Hat das quadratische Glied den Koeffizienten 1, spricht man von der Normalform der quadratischen Gleichung (a=1). Definieren wir p=ba und q=ca, dann lässt sich die Normalform auch ausdrücken als x²+px+q=0.

Die berühmte 🏆 PQ-Formel lautet nun:

In diese Formel kannst du die Koeffizienten deiner zu lösenden quadratischen Gleichung einsetzen. In unserem Beispiel waren das a=5, b=3, c=-54

Durch die Vorzeichen beziehungsweise den Operanden ergeben sich die Lösungen

x₁=3

x₂=-3

L={3;-3}

Wieso gibt es zwei Werte in der Lösungsmenge? 💥 Ganz einfach: Die einfache quadratische Gleichung x²=64 gibt Aufschluss. Um diese zu lösen, ziehst du auf beiden Seiten die Wurzel, sodass sich x=8 ergibt. Der Wert im Quadrat gilt aber auch bei negativen Vorzeichen! Deswegen ist x²=64für 8 und -8 wahr.

Nullstellen der quadratischen Gleichungen

Die Lösung der quadratischen Gleichung ist ein Wert, für den die Gleichung wahr ist, wenn er als Unbekannte eingesetzt wird. Für die reellen Zahlen kann eine quadratische Gleichung keine, eine oder zwei Zahlen in der Lösungsmenge enthalten.

Warum? 🤓 Stell dir die Gleichung als Schaubild - als Parabel - vor. Diese kann die Null-Achse in keinem Punkt berühren oder in genau einem, sie kann die Achse aber auch in zwei Punkten schneiden. Diese Stellen sind die Nullstellen.

Mit der sogenannten Diskriminante (von lat. discriminare = unterscheiden) kannst du die Anzahl der Nullstellen bestimmen. Die allgemeine Formel lautet:

D=b²-4ac

D=p²-4q ist die normierte Darstellung

• Diskriminante positiv: 2 Nullstellen, 2 Lösungen x1 und x2
• Diskriminante Null: 1 Nullstelle, eine (doppelte) Lösung
• Diskriminante negativ: keine Nullstelle, keine reelle Lösung der quadratischen Gleichung L=

Was ist mit den binomischen Formeln?

Bestimmt erinnerst du dich an die binomischen Formeln aus der Algebra, mit denen sich Produkte aus Binomen umformen lassen beziehungsweise die das Umformen von Klammern erleichtern und dir bei der Faktorisierung von Termen helfen. 📐  Ähnlich wie bei der Mitternachtsformel wollen die meisten Lehrer, dass du die Dreieinigkeit der drei binomischen Formeln im Schlaf 🥱 hersagen kannst:

1. (a+b)²=a²+2ab+b²
2. (a-b)²=a²-2ab+b²
3. (a+b)(a-b)=a²-b²

Die binomischen Formeln helfen dir bei einem Spezialfall der quadratischen Gleichungen, nämlich bei der sogenannten quadratischen Ergänzung. Dazu formst du die Gleichung so um, dass du links x²+2dx erhältst. Addierst du nun d² (quadratische Ergänzung), hast du links einen Term, den du mit der binomischen Formel umformst. Das Ergebnis ist eine leicht nach x aufzulösende Gleichung.

3x²-15x+18=0

Du teilst durch den Leitkoeffizienten (a=3), um die Normalform zu erhalten:

x²-5x+6=0

Dann subtrahierst du das konstante Glied (c=6), damit es rechts steht:

x²-5x=-6

Jetzt nimmst du die quadratische Ergänzung vor und addierst auf beiden Seiten die Hälfte des Koeffizienten im Quadrat.

Die rechte Seite kannst du einfach ausrechnen, die Linke mit der binomischen Formel umformen:

Anschließend ziehst du auf beiden Seiten die Wurzel und kannst nach x auflösen. Es ergibt sich:

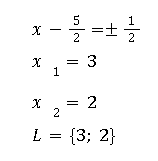
Was sind nochmal die binomischen Formeln? Diese und weitere Fragen kannst du in einem Mathe-Quiz für Kinder stellen!

Lösung von Bruchgleichungen: Variable im Zähler oder Nenner

Bruchgleichungen können Unbekannte im Zähler oder Nenner haben. Wie löst du diese Gleichungen?

Variable im Zähler des Bruches

Sieh dir dieses Beispiel einer Gleichung an:

Zur einfachen Lösung ist es am besten, wenn du die komplizierten Bruchstriche loswirst. Dazu kannst du beide Seiten mit beiden Nennern multiplizieren, in unserem Beispiel also 8 und 3.

Jetzt kannst du die Klammern ausrechnen und durch die Äquivalenzumformung nach x auflösen.

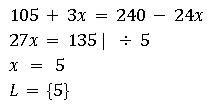
Variable im Nenner des Bruches

Findest du die Variable im Nenner, musst du die Gleichung wieder umformen und multiplizierst daher beide Terme mit der Variable und ihrem Koeffizienten:

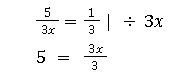
Jetzt kannst du bequem nach x auflösen.

x = 5

L={5}

Polynome in Gleichungen lösen

Schwieriger wird es mit Gleichungen, die höhere Potenzen als Zweierpotenzen enthalten. Ein Polynom dritten Grades und höher enthält also eine Unbekannte mit dritter oder höherer Potenz: x³. 

Eine solche Gleichung musst du zunächst derart umformen, dass du nur noch eine quadratische Gleichung zu lösen hast. 🧠 Diese kannst du wie im obigen Beispiel mit der PQ-Formel auflösen. 

Das Umschreiben einer Gleichung mit Polynomen höheren Grades erfordert die Linearfaktorzerlegung, also die Polynomdivision. Das Ausklammern kann dir hier eine Hilfe sein. 🦮

Die verbleibende quadratische Gleichung löst du mit der PQ-Formel.

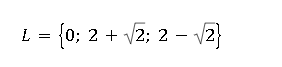
Hast du noch Fragen? Dann buche eine kostenlose Mathe Nachhilfe Stunde mit einem unserer Mathematik Nachhilfelehrern. 

Alle Unklarheiten beseitigt? Dann bist du ja jetzt bereit für die nächste Mathe-Prüfung! Hast du dennoch Prüfungsangst, geben wir dir ein paar Tipps, wie du entspannt an die Sache herangehst.