Kapitel:
- Brüche kürzen einfach erklärt
- Brüche kürzen: 3 simple Regeln
- Brüche Kürzen üben mit diesen Beispielen
- Fazit: Das Kürzen von Brüchen kann einfach sein
Mathe und Bruchrechnen bereiten dir in der Schule Schwierigkeiten? Wir versprechen dir: Mit unseren 3 einfachen Regeln, ist Brüche kürzen bald kein Problem mehr für dich. 🤗
Hier zeigen wir dir alles was du dazu wissen musst. 🤘 Anschließend gibt es ein paar Beispielaufgaben zum Brüche Kürzen.
Du möchtest davor nochmal die Grundlagen vom Bruchrechnen überfliegen? Dann schau doch einfach in unseren Artikel vorbei - hier haben wir Bruchrechnen einfach erklärt. Viel Erfolg! 😎
Brüche kürzen einfach erklärt
Das Brüche Kürzen verwendest du beim Addieren und Subtrahieren von nicht gleichnamigen Brüchen. 💡 Zur Erinnerung: Nicht gleichnamige Brüche sind solche, wo die Nenner der beiden Brüche (also die untere Zahl des Bruchs) nicht die gleich ist. 🧐
Bei gleichnamigen Brüchen ist die Addition und Subtraktion sehr einfach. Du musst einfach nur die Nenner der Brüche addieren oder subtrahieren. Hier sind ein paar Beispiele:
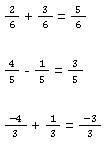
Das liegt daran, dass du ja gleichartige Teile miteinander verrechnen willst. Isst du zwei Viertel einer Pizza, hast du eine halbe Pizza gegessen. Also bleiben dir noch 4 - 2 = 2 Teile übrig. 🍕
Wenn die Nenner nicht gleich sind, wird diese Rechnung schwieriger. Isst du zum Beispiel ein Viertel und ein Drittel, musst du erst einmal überlegen, wie viel du gegessen oder übrig hast. 😅
Generell gibt es bei ungleichnamigen Brüchen zwei Möglichkeiten zur Berechnung, das Erweitern und das Kürzen. Wir fokussieren uns ab hier auf das Kürzen. 🔬
Das ist ein Beispiel für einen ungleichnamigen Bruch:
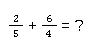
In diesem Fall musst du die Nenner erst einmal angleichen, damit die Addition oder auch Subtraktion möglich ist. ⚖️
Zusätzlich wird das Brüche Kürzen auch verwendet, um große Zahlen bei der Multiplikation und Division zu verkleinern. Denn 2356 * 342 rechnen die meisten Menschen nicht mehr einfach so im Kopf aus. 🤯
Brüche kürzen: 3 simple Regeln
Die Erweiterung von Brüchen verwendet man eher bei kleineren Zahlen. Bei größeren bietet sich eher das Kürzen an. Generell solltest du dafür die folgenden Regeln beachten um den Nenner gleich zu machen. Sobald das passiert ist, kannst du wie bekannt einfach normal addieren oder subtrahieren. 👻
✅ 1. Dividiere jeweils Zähler und Nenner eines Bruches
Du musst für jeden einzelnen Bruch je Zähler und Nenner nehmen und durch die gleiche Zahl größer als 1 teilen. Nehmen wir einmal dieses Beispiel:
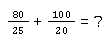
Das Ziel dieser Rechenoperation ist es, dass die beiden Nenner gleich sind. Die Zahl, durch die du den Zähler und Nenner teilst, muss nicht für beide Brüche gleich sein!
Wonach du hier suchen musst, das nennt sich der größte gemeinsame Teiler. Welche Zahl haben 25 und 20 gemeinsam? Durch welche Zahl musst du beide Nenner teilen, um auf das gleiche Ergebnis zu kommen?
Um diesen größten, gemeinsamen Teiler zu finden, schreibst du einfach alle Teiler einer Zahl auf:
25 = (1, 5, 25)
100 = (1, 2, 4, 5, 10, 20, 25, 50, 100)
Was ist der größte, gemeinsame Teiler?
….richtig, der größte, gemeinsame Teiler ist 5.
Dafür musst du die 25 durch 5 und die 20 durch 4 teilen. Und natürlich die 80 ebenfalls durch 5 und die 100 ebenfalls durch 4:
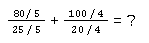
Als Ergebnis hast du dann:
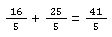
Beachte, dass das Kürzen nicht den Wert des Bruches verändert. Du schreibst lediglich den Bruch auf eine andere Weise. Das ist genauso wie eine halbe Pizza und zwei Viertel Pizzen - beides ist die gleiche Menge. 😜
✅ 2. Durch einige Zahlen darfst du nicht teilen
Du solltest dir merken, dass du beim Kürzen keine Zahl durch 0 teilen kannst. Außerdem solltest du nicht durch eine negative Zahl teilen. Zuletzt macht es natürlich meist auch keinen Sinn durch die Zahl selbst zu teilen, weil sonst 1 als Ergebnis kommt. 🤪
✅ 3. Wenn kürzen nicht funktioniert, dann funktioniert erweitern
Wenn die Nenner so klein sind, dass du keinen größten, gemeinsamen Teiler finden kannst, dann funktioniert das Kürzen natürlich nicht. In diesem Fall kannst du aber mit dem Erweitern trotzdem eine Lösung finden. 🤠
Brüche kürzen üben mit diesen Beispielen
Damit du das Kürzen wirklich verstehst, haben wir dir hier ein paar Beispielaufgaben mit Lösungen zusammengestellt. 🤗
Beispielaufgaben Brüche kürzen
Brüche kürzen bei der Addition
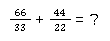
Brüche kürzen bei der Subtraktion
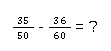
Brüche kürzen bei der Multiplikation
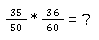
Brüche kürzen bei der Division
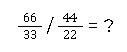
Lösungen
Brüche kürzen bei der Addition
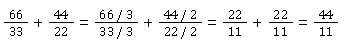
Brüche kürzen bei der Subtraktion
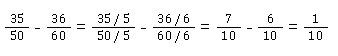
Brüche kürzen bei der Multiplikation
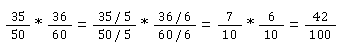
Brüche kürzen bei der Division
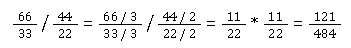
Fazit: Das Kürzen von Brüchen kann einfach sein
Du siehst - es ist wirklich nicht schwer, zu kürzen. Jetzt weißt du alles, was wichtig ist, um bei ungleichnamigen Brüchen mit der Addition und Subtraktion sowie zur Vereinfachung von Multiplikation und Division zu rechnen. 🤭
Wenn du nochmal die allgemeine Bruchrechnung nachlesen möchtest, schau dir unseren Artikel an. Oder wie wäre es einmal mit ein paar Mathe-Quiz oder Mathe-Apps? Viel Spaß beim Ausprobieren! 🥳