Kapitel:
- Addieren von gleichnamigen Brüchen: So geht’s
- Ungleichnamige Brüche addieren
- Brüche addieren: Aufgaben zum Üben
- Du brauchst Hilfe beim Bruchrechnen? GoStudent hilft dir
- Fazit: Brüche addieren kann jeder
Spätestens beim Bruchrechnen fangen für viele Schüler die Probleme in der Schule an. 🤨 Tatsächlich brauchst du aber für die Bruchrechnung und speziell für die Addition kaum Mathematik! 🤓
Lerne in diesem Artikel die 7 wichtigsten Regeln zum Brüche addieren. Einfach erklärt und mit Übungsaufgaben. So bestehst du den nächsten Mathe-Test bestimmt! Viel Spaß dabei! 🥳
Du fängst beim Bruchrechnen ganz von vorne an? Dann lese dir zuerst diesen Artikel über die Grundlagen der Bruchrechnung durch.
1. Addieren von gleichnamigen Brüchen: So geht’s
Bei einem Bruch gibt es drei Bestandteile: Der Zähler ist oben und gibt die Gesamtzahl der Teile an, die wir zählen. Der Nenner ist unten und beschreibt die existierenden Teile des Ganzen: Eine Viertel Pizza zeigt zum Beispiel, dass es ein Stück einer Pizza aus vier Teilen ist. 🍕 Die beiden Zahlen werden in der Mitte durch den Bruchstrich getrennt. So weit so gut.
Für Brüche mit dem gleichen Nenner gibt es die Bezeichnung gleichnamiger Bruch. Hier siehst du ein Beispiel für so einen Bruch:
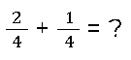
In Diesem Fall musst du lediglich die Zähler zusammenrechnen. 2 + 1 = 3. Also ist das Ergebnis:
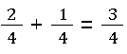
Der Nenner bleibt gleich, du musst hier absolut nichts berechnen. So lange die beiden Nenner gleich sind, haben wir also einen gleichnamigen Bruch.
Natürlich gibt es eine ganze Reihe von weiteren Details, wie addierte Brüche komplexer werden können. Diese findest du hier einzeln erklärt - einfach und übersichtlich. 🧐
Regel 1 - Gemischte Brüche addieren
✅ Wir verstehen unter einem gemischten Bruch, dass vor dem Bruch noch eine natürliche Zahl (1, 2, 3, etc.) steht. Ein Beispiel für einen gemischten Bruch ist:
![]()
Gemischte Brüche müssen immer erst einmal umgewandelt werden. Dafür braucht es grundlegende Multiplikation:
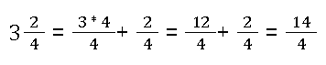
Diese 14 Viertel kannst du anschließend noch auf 7 Halbe kürzen.
Also können wir nun eine gleichnamige Addition mit einem gemischten Bruch kalkulieren:
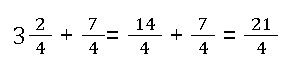
Regel 2 - Brüche mit ganzen Zahlen addieren
✅ Anders als bei gemischten Brüchen steht zwischen der Zahl und dem Bruch ein mathematischer Operator, bei der Addition also ein Pluszeichen. Hier findest du ein Beispiel:
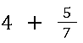
Diese ganze Zahl wird ganz einfach in einen Bruch umgewandelt. Egal welche Zahl davor steht - du nimmst die Zahl als Zähler und stellst eine 1 als Nenner darunter. Denn eine 4 ist nichts anderes als 4 Ganze:
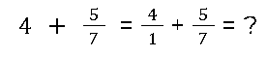
Wie du siehst, ist der Nenner bei diesem Beispiel nicht wie beim zweiten Bruch. Also kannst du nicht wie bereits gelernt vorgehen, sondern musst den Bruch entweder erweitern oder kürzen. 💁 Das lernst du weiter unter, du kannst auch direkt dorthin springen.
Regel 3 - Brüche mit negativen Zahlen addieren
✅ Im nächsten Schritt addieren wir mit negativen, natürlichen Zahlen (-1, -2, -3, etc.). Auch dies ist kein Hexenwerk, wie du sehr schnell begreifen wirst!
Nehmen wir einmal die folgende Aufgabe:
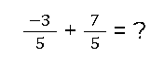
Wie wird das berechnet? Wenn wir -3 nehmen, sind wir im negativen Bereich der natürlichen Zahlen. Fügen wir dazu die 7 hinzu, eine positive Zahl, dann ergibt sich daraus +4, also eine positive Zahl für den Zähler. Das Ergebnis ist also:
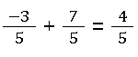
Genauso wird auch bei negativen Dezimalzahlen vorgegangen.
Regel 4 - Brüche mit Dezimalzahlen addieren
✅ Eine Dezimalzahl ist eine natürliche positive oder negative Zahl (1, 2, 3, etc.) mit einem Komma und weiter dahinter stehenden Zahlen. Beispiele für Dezimalzahlen sind:
- 3,4
- 2,6
- -5,7
- -2,8
Wie verhält es sich daher mit einer Addition von Brüchen, die über Dezimalzahlen verfügen?
Ein Beispiel für ein solche Aufgabe ist:
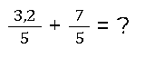
Die Addition funktioniert hier genauso wie bereits gelernt. Du rechnest also 3,2 + 7 = 9,2 für den Zähler. Das Ergebnis wird dann wie folgt berechnet:
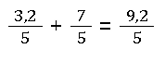
Auch mit negativen Zahlen funktioniert das wie bereits gelernt. Siehe dazu die Beispielaufgabe:
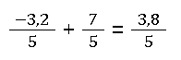
Selbst wenn du hier einen gemischten Bruch oder einen mit ganzen Zahlen hast, ändert sich die Vorgehensweise auch nicht. 😆
Regel 5 - Drei oder mehr Brüche addieren
✅ Natürlich bestehen nicht alle Bruchrechenaufgaben mit Addition aus nur zwei Brüchen. Selbstverständlich kannst du 3 oder mehr Brüche miteinander addieren. Die Berechnung ändert sich aber nicht. So ist das Ergebnis der folgenden Rechnung wie erwartet:
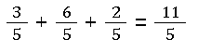
Denn 3 + 6 + 2 = 11.
2. Ungleichnamige Brüche addieren
Bis jetzt haben wir nur gleichnamige Brüche addiert, bei denen der Nenner, also der untere Bruch-Bestandteil stets gleich geblieben ist. 😳 Wenn die Nenner unterschiedlich sind, sprechen wir von einem ungleichnamigen Bruch. Hier siehst du ein Beispiel:
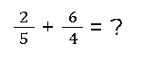
Denn anders als beim gleichnamigen Bruch kannst du nicht einfach 2 und 6 addieren. Die Herausforderung bei ungleichnamigen Brüchen ist, dass du die Nenner erst einmal aneinander angleichen musst, bevor die beiden Brüche verrechnet werden können.
Dafür gibt es grundsätzlich zwei Möglichkeiten, das sogenannte erweitern und das sogenannte Kürzen. Beide findest du im folgenden erklärt:
Regel 6 - Brüche erweitern
✅ Erweitern ist eine gute Idee, besonders wenn die Nenner klein sind. Anstatt große Nenner zu kürzen, solltest du sie verkürzen. Hier ist eine Illustration: Nehmen wir an, wir wollen zwei Viertel mit drei Fünfteln addieren.
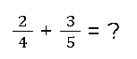
Da die Nenner von 4 und 5 unterschiedlich sind, müssen wir beide Brüche mit einer Zahl multiplizieren, um die Nenner anzugleichen. Versuchen wir es mal:
Das kleinste gemeinsame Vielfache der Nenner ist die beste Methode, um die Antwort zu finden. Wenn die Nenner 4 und 5 mit den Zahlen 1, 2, 3, 4, 5, 6 multipliziert werden, ist das Ergebnis 20 für die Zahl 4 mit dem Multiplikator 5. Der Multiplikator 4 multipliziert mit der Zahl 5, um die Zahl 20 zu erhalten.
Wichtig: Weder der Nenner noch der Zähler sollte beim Multiplizieren eine Dezimalzahl sein. Wenn das nicht funktioniert, versuche es stattdessen mit dem Kürzen. Außerdem kann die Zahl 0 nicht multipliziert werden. Du kannst addieren, sobald die Nenner gleich sind, wie zuvor gezeigt.
💡 Du brauchst noch mehr Hilfe beim Multiplizieren von Brüchen? In diesem Artikel haben wir Brüche multiplizieren einfach erklärt.
Regel 7 - Brüche kürzen
✅ Bei größeren Brüchen müssen wir es andersherum machen. Wenn du einen Bruch kürzt, teilst du den Zähler und den Nenner durch eine Zahl größer als 1. Das gilt vor allem, wenn es um extrem große Brüche geht. 📶
Nehmen wir an, du musst diese beiden Brüche addieren:
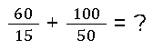
Wir müssen die Nenner angleichen, da sie nicht gleich sind. Erweitern ist keine gute Idee, da du sonst eine Menge Multiplikationen durchführen musst. Deshalb versuchen wir, die Zahlen so klein wie möglich zu halten.
Wir könnten das zum Beispiel auf die Zahl 5 reduzieren. Der erste Bruch kann durch 3 und der zweite Bruch durch 10 geteilt werden. Danach kannst du diese beiden Zahlen einfach addieren oder subtrahieren. Du kannst nicht durch Null dividieren, vergiss das nicht!
Wichtig: Weder der Nenner noch der Zähler dürfen beim Dividieren eine ungerade ganze Zahl sein. Wenn es nicht klappt, versuche stattdessen zu expandieren. Nachdem der Nenner wieder gleich ist, kannst du wie oben gelernt addieren.
3. Brüche addieren: Aufgaben zum Üben
Für jedes Beispiel bekommst du eine Übungsaufgabe und eine Lösung. Wir wünschen dir viel Erfolg!
Normales Addieren
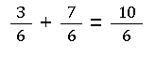
Gemischte Brüche addieren
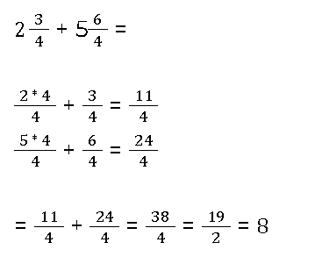
Brüche mit ganzen Zahlen addieren
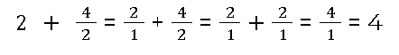
Brüche mit negativen Zahlen addieren
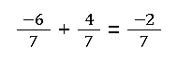
Brüche mit Dezimalzahlen addieren
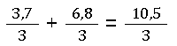
Drei oder mehr Brüche addieren
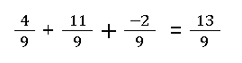
Brüche erweitern
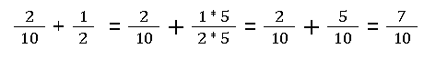
Brüche kürzen
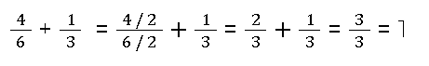
4. Du brauchst Hilfe beim Bruchrechnen? GoStudent hilft dir
Wenn du Schwierigkeiten hast, mit deinen Mitschülern in Mathe mitzuhalten, bist du nicht allein. Oder stehst du kurz vor deinen Mathe-Prüfungen für das Abitur? Dann können wir dir helfen. 💆
Bei GoStudent findest du deinen idealen Mathe-Nachhilfelehrer, der sich genau an deine speziellen Lernbedürfnisse anpasst. So bekommst du dein Selbstvertrauen in Mathe zurück. 🧘♂️ Buche jetzt eine kostenlose Probestunde und teste unsere GoStudent Mathe-Nachhilfe. 🤩
5. Fazit: Brüche addieren kann jeder
Bruchrechnung ist einfach zu lernen. Wir haben dir hier alles gezeigt, was du für die Addition von Brüchen wissen und verstehen musst. Jetzt heißt es üben, üben, üben. Viel Erfolg bei der Addition von Brüchen. 😻