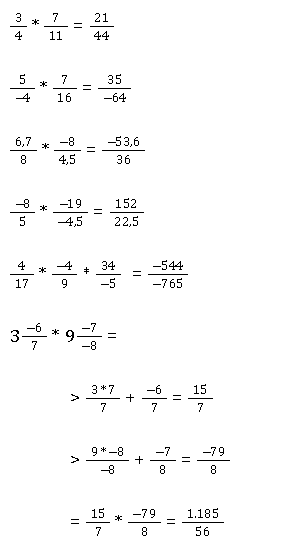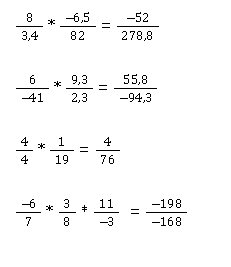Kapitel:
- Multiplizieren von Brüchen: So geht’s
- Brüche erweitern
- Brüche multiplizieren: Aufgaben zum Üben
- Bruchrechnen online lernen mit GoStudent
- Fazit: Brüche multiplizieren ist einfach, wenn gewusst wie
Brüche multiplizieren ist schwierig und im echten Leben nutzlos? Weit gefehlt - Dieser Teil der Bruchrechnung ist einfach zu lernen und wird auch bei anderen Rechenarten häufig benötigt - zum Beispiel um Brüche bei Addition und Subtraktion zu erweitern. 😯
Darum pass jetzt gut auf - in diesem Artikel erklären wir dir leicht verständlich die wichtigsten Regeln zum Brüche multiplizieren. Du hast zuvor noch Fragen zu den Grundlagen der Bruchrechnung? Hier haben wir Bruchrechnung einfach erklärt. Viel Erfolg und viel Spaß! 😎
1. Multiplizieren von Brüchen: So geht’s
Brüche können auf einfache Weise multipliziert werden. Es macht keinen Unterschied, ob der Zähler und der Nenner gleich sind. 👆 Du musst also davor nicht erweitern oder kürzen. 👀 Es macht auch keinen Unterschied, ob du einen echten oder einen unechten Bruch hast. (Echte Brüche haben Nenner, die größer sind als die Zähler, während unechte Brüche Nenner haben, die kleiner sind als die Zähler.)
Nehmen wir einmal das folgende Beispiel für die Multiplikation:
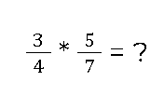
Um diese beiden Brüche miteinander zu multiplizieren, musst du lediglich die beiden Nenner sowie die Zähler getrennt voneinander multiplizieren.
Das sieht dann so aus:
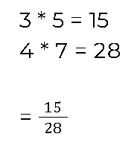
Multiplizieren von gemischten Brüchen
Wie sieht das ganze nun mit gemischten Brüchen aus? 🤷♂️ Gemischte Brüche haben vor dem eigentlichen Bruch noch eine natürliche Zahl.
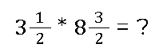
Gemischte Brüche müssen erst einmal umgewandelt 🔄 werden. Das geht ganz schnell - keine Sorge.
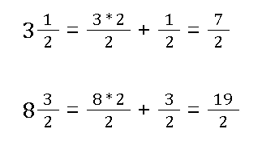
Anschließend müssen wir nur noch diese beiden Brüche normal miteinander multiplizieren
Multiplizieren mit negativen Zahlen
Bei der Multiplikation von positiven und negativen Zahlen (-1, -2, -3 usw.) gelten die Vorzeichenregeln. Diese sind:
- Positiv und positiv ergibt positiv ➕
- Positiv und negativ ergibt negativ ➖
- Negativ und positiv ergibt negativ ➖
- Negativ und negativ ergibt positiv ➕
Wie wird also die folgende Aufgabe gelöst?
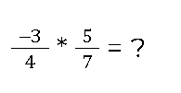
Die Berechnung -3 * 5 muss eine negative Zahl zur Folge haben, weil negative und positive Vorzeichen zu einem negativen Ergebnis führen. Da 3 multipliziert mit 5 die Zahl 15 als Ergebnis haben, müssen wir davor ein negatives Vorzeichen einfügen: -15
Das Ergebnis ist also
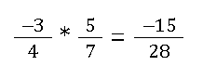
Multiplizieren mit Dezimalzahlen
Auch die Multiplikation von Brüchen mit Dezimalzahlen ist sehr einfach. Bei Dezimalzahlen gibt es Kommastellen, also 2,4 oder 5,7. 😎
Die Berechnung erfolgt einfach wie schon oben gelernt:
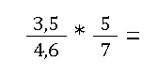
Hier werden wir also 3,5 mit 5 multiplizieren, das ergibt 17,5. Rechnen wir die Aufgabe komplett durch, landen wir dementsprechend beim Ergebnis:
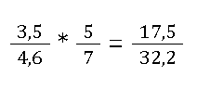
Die Rechnung wird auch durch negative Zahlen oder gemischte Zahlen nicht verändert.
Multiplizieren mit drei oder mehr Brüchen
Wie machen das ganze nun noch komplizierter! Statt zwei Brüchen werden wir jetzt drei miteinander verrechnen. 🤗
Zum Beispiel:
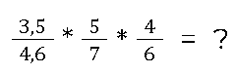
Wir können hier ganz einfach alle drei Zähler und Nenner jeweils miteinander multiplizieren. Wir rechnen 3,5 * 5 * 4 = 70 und 4,6 * 7 * 6 = 193,2.
Es gibt noch einen Sonderfall. Wenn drei Brüche miteinander verrechnet werden sollen und neben einer Multiplikation zum Beispiel eine Addition da ist, dann gilt die Regel ,,Punkt vor Strichrechnung”. Zum Beispiel:
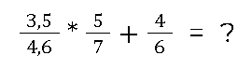
Da Punkt vor Strichrechnung gilt, müssen zuerst die beiden ersten Brüche multipliziert werden. Erst danach wird das Ergebnis mit dem letzten Bruch addiert.
2. Brüche erweitern
Wenn die Nenner der Brüche bei der Addition und Subtraktion nicht gleich sind, können die Brüche erweitert oder gekürzt werden. Wenn die Zähler kleiner sind als die Nenner, wird die Erweiterung angewendet. Um diese Probleme zu lösen, ist die Multiplikation erforderlich. Was genau bedeutet das?
Nehmen wir einmal diese Rechenaufgabe:
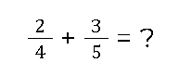
Diese kann man nicht einfach nach den Regeln der Addition berechnen. Also muss man wie folgt vorgehen:
Das kleinste gemeinsame Vielfache der Nenner ist die beste Methode, um die Antwort zu finden. Wenn die Nenner 4 und 5 mit den ganzen Zahlen 1, 2, 3, 4, 5, 6 multipliziert werden, ist das Ergebnis 20 für die 4 mit dem Multiplikator 5. Der Multiplikator 4 multipliziert die Zahl 5, um die Zahl 20 zu erhalten.
Wichtig: Weder der Nenner noch der Zähler dürfen beim Multiplizieren eine Dezimalzahl (Zahl mit Komma) sein. Wenn das nicht funktioniert, versuche es stattdessen mit dem Kürzen. 🙆
Du kannst jetzt wie gewohnt mit Addition und Subtraktion fortfahren.
3. Brüche multiplizieren: Aufgaben zum Üben
Hier geben wir dir für jedes Beispiel noch eine Aufgabe zum Üben und mit Lösung mit auf den Weg. Außerdem findest du unten zusätzlich noch ein Übungsblatt mit weiterführenden Aufgaben. Viel Erfolg!
Normales Multiplizieren
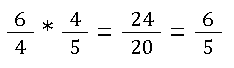
Multiplizieren mit gemischten Zahlen
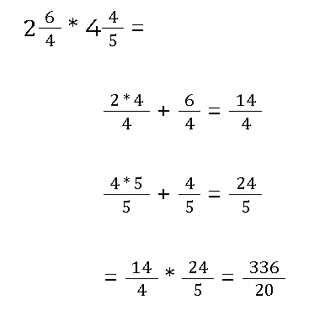
Multiplizieren mit negativen Zahlen
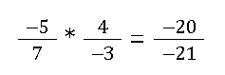
Multiplizieren mit Dezimalzahlen
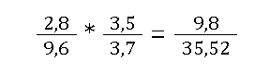
Multiplizieren mit drei oder mehr Brüchen
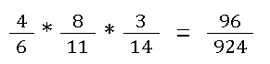
Multiplizieren mit gemischten Operationen
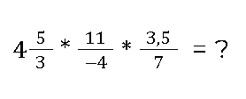
Wir berechnen zuerst den gemischten Bruch
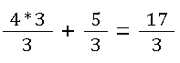
Und dann den Rest
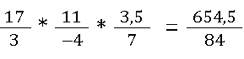
4. Bruchrechnen online lernen mit GoStudent
Fällt es dir schwer, allein mit deinen Mitschülern in Mathe mitzuhalten? Stehst du kurz vor den Abiturprüfungen in Mathe? Willst du manchmal einfach aus dem Klassenzimmer gehen und nach Hause gehen, 🏃♀️ wenn es um Brüche oder andere Herausforderungen geht? Die Hilfe eines Mathe-Nachhilfelehrers von GoStudent kann auch in dieser Situation sehr wertvoll sein.
Mit GoStudent hast du die Möglichkeit, dich regelmäßig mit einem Nachhilfelehrer in einem virtuellen Klassenzimmer zu treffen. Die Nachhilfestunden werden auf deine individuellen Bedürfnisse zugeschnitten und helfen dir, deine Wissenslücken zu schließen und in der Mathematik wieder auf Kurs zu kommen. 😇
Darüber hinaus bist du eingeladen, einen kostenlosen Probeunterricht zu besuchen, um zu sehen, wie gut es dir gefällt. Um loszulegen, musst du nur das Anmeldeformular ausfüllen. Einer unserer Mathe-Nachhilfelehrer wird sich so schnell wie möglich mit dir in Verbindung setzen, damit du so schnell wie möglich mit der Mathe-Nachhilfe beginnen kannst. 🤠
Übrigens - beim Mathe lernen können dir auch Quizze oder Apps behilflich sein!
5. Fazit: Brüche multiplizieren ist einfach, wenn man weiß wie
Jetzt weißt du ganz genau, wie das Berechnen von Brüchen mit Multiplikationen funktioniert - und zwar in jedem Fall. Damit du das ganze noch Üben kannst, haben wir dir Beispielaufgaben angehängt. Wenn du außerdem noch einmal das ganze Thema wiederholen möchtest, kannst du dir den Hauptartikel zur Bruchrechnung hier noch einmal anschauen. 😍
Bevor du dir die Lösungen anschaust, versuche bitte zuerst, die Aufgaben selbst zu bearbeiten. Du lernst mehr, wenn du die Lösungen danach zu Rate nimmst, als wenn du die Lösungen einfach nur nachvollziehen möchtest. Lege dich also idealerweise nicht selbst rein!
Brüche multiplizieren üben: Aufgaben
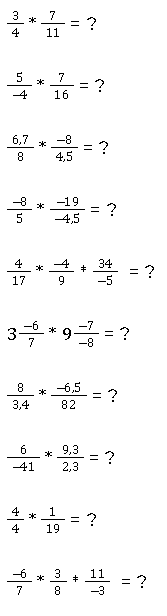
Die Lösungen: