Kapitel:
- Was ist ein Bruch: Grundbegriffe
- Brüche erweitern: So geht’s!
- Brüche erweitern: Beispiele & Übungen!
Brüche erweitern und das kleinste gemeinsame Vielfache bestimmen? In diesem Artikel helfen wir dir beim Bruchrechnen auf die Sprünge und verraten dir, wie das Erweitern von Brüchen funktioniert. Es ist gar nicht so kompliziert ‒ versprochen! 😉 🧮 ⬇️
Was ist ein Bruch: Grundbegriffe
Das Bruchrechnen ist ein Teilgebiet der Mathematik, das Schüler die ganze Schulzeit lang begleitet. 🧑🎓
Beim Bruchrechnen geht es um das Verhältnis eines Ganzen zu seinen Teilen. Nehmen wir als Beispiel eine Pizza: Du möchtest sie mit deinen Schulkollegen teilen und schneidest die Pizza deshalb in 10 gleiche Stücke. Du hast 6 Freunde zu dir eingeladen ‒ jeder von ihnen und auch du bekommen eines der 10 Pizzastücke. Gemeinsam esst ihr also 7 von 10 Teilen - oder sieben Zehntel der Pizza. 🍕
Mit Zahlen wird das folgendermaßen geschrieben: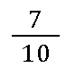
Die Zahl oben, über dem Bruchstrich, wird auch als Zähler bezeichnet. Bei unserem Beispiel ist 7 der Zähler. Die Zahl unter dem Bruchstrich ist der sogenannte Nenner ‒ in unserem Fall die 10. Der Nenner gibt an, in wie viele Teile das Ganze geteilt wurde. Und der Zähler, wie viele Teile in unserem speziellen Fall gemeint sind. Der Bruchstrich in der Mitte zeigt uns, dass geteilt wird. 💡
Erfahre noch mehr über Brüche in unserem Artikel über das Bruchrechnen. Inklusive toller Übungen und eines gratis Aufgabenblattes! 👍
Damit du Brüche subtrahieren und addieren kannst, brauchst du gleichnamige Brüche. So werden Brüche bezeichnet, die einen gemeinsamen Nenner haben.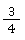 und
und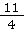 sind zum Beispiel gleichnamige Brüche. Bei beiden steht unter dem Bruchstrich eine 4. ✅
sind zum Beispiel gleichnamige Brüche. Bei beiden steht unter dem Bruchstrich eine 4. ✅
Wenn Brüche nicht denselben Nenner haben, du aber trotzdem mit ihnen rechnen möchtest, musst du sie zuerst umformen und auf einen gemeinsamen Nenner bringen. Das klappt zum Beispiel, indem du die Brüche erweiterst: ⬇️
Brüche erweitern: So geht’s!
Einen Bruch kannst du erweitern, indem du Zähler und Nenner mit derselben Zahl multiplizierst. Zum Beispiel hier mit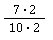
Der Wert der Bruchzahl ändert sich dadurch jedoch nicht: Der vom Bruch dargestellte Anteil bleibt derselbe ‒ er wird nur in kleinere Abschnitte unterteilt. Wenn du zum Beispiel Zähler und Nenner von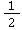 mit 2 multiplizierst, kommt dabei
mit 2 multiplizierst, kommt dabei 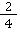 heraus.
heraus.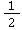 und
und 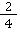 haben denselben Wert. Nur wird das Ganze bei
haben denselben Wert. Nur wird das Ganze bei 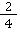 in mehrere Teile unterteilt (in unserem Fall in doppelt so viele, weil wir mal 2 gerechnet haben) und zugleich auch mehrere Teile ausgewählt (auch doppelt so viele). 🤔
in mehrere Teile unterteilt (in unserem Fall in doppelt so viele, weil wir mal 2 gerechnet haben) und zugleich auch mehrere Teile ausgewählt (auch doppelt so viele). 🤔
Anhand eines Tortendiagramms ist das sehr gut zu erkennen. Der blaue Teil des Diagramms zeigt die halbe Pizza (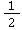 ): ⬇️
): ⬇️
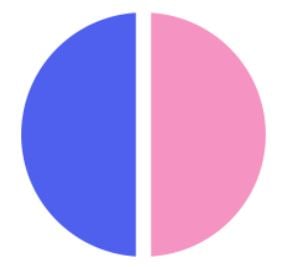
Hier zeigt der blaue Teil zwei Viertel der Pizza (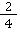 ): ⬇️
): ⬇️
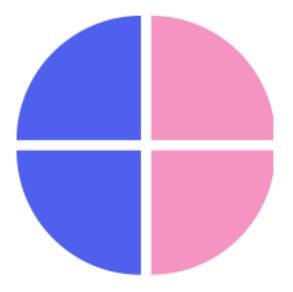
Beide Teile (sowohl die Hälfte als auch zwei Viertel) sind gleich viel. Es ist ganz egal, ob du von der Pizza 1 von 2 Stücken nimmst oder 2 von 4. Du hast jedes Mal die halbe Pizza. 🍕 😉
Merke dir also: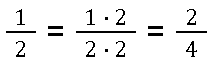
Brüche auf einen gemeinsamen Nenner zu bringen, gelingt auch, indem du die Brüche kürzt. Das Kürzen von Brüchen ist genau das Gegenteil vom Erweitern von Brüchen.
Schauen wir uns jetzt ein paar Übungsbeispiele an, damit das Erweitern von Brüchen für dich ein Kinderspiel wird: ⬇️
Brüche erweitern: Beispiele & Übungen!
1. Übung: Brüche erweitern mit Vorgabe
🧠 Aufgabenstellung: Erweitere den Bruch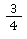 mit 5.
mit 5.
💡 Anleitung: Zähler und Nenner müssen jeweils mit 5 multipliziert werden.
🧮 Rechnung: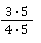
✅ Lösung: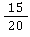
Das war noch ganz einfach, nicht wahr? Gehen wir jetzt einen Schritt weiter: ⬇️
2. Übung: Brüche erweitern ohne Vorgabe
🧠 Aufgabenstellung: Der Bruch 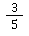 soll so erweitert werden, dass im Nenner die Zahl 15 steht. Mit welcher Zahl muss der Bruch erweitert werden? Und wie lautet der Bruch am Ende?
soll so erweitert werden, dass im Nenner die Zahl 15 steht. Mit welcher Zahl muss der Bruch erweitert werden? Und wie lautet der Bruch am Ende?
💡 Anleitung: Überlege zuerst, mit welcher Zahl 5 multipliziert werden muss, damit im Nenner 15 steht. Wenn du das herausgefunden hast, multipliziere sowohl Zähler als auch Nenner mit dieser Zahl!
🧮 Rechnung: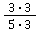
✅ Lösung: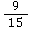
Jetzt hast du die Erweiterungszahl zum ersten Mal selbst herausgefunden. Das üben wir gleich noch einmal: ⬇️
3. Übung: Gemeinsamen Nenner finden
🧠 Aufgabenstellung: Bringe die Brüche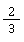 und
und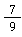 auf einen gemeinsamen Nenner!
auf einen gemeinsamen Nenner!
💡 Anleitung: Überlege, mit welcher Zahl du den kleineren Nenner des ersten Bruchs multiplizieren musst, damit er 9 wird. Da 3 · 3 = 9, musst du den Bruch einfach mit der Erweiterungszahl 3 multiplizieren!
🧮 Rechnung: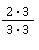
✅ Lösung: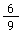 und
und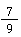 haben den gemeinsamen Nenner 9.
haben den gemeinsamen Nenner 9.
4. Übung: Gemeinsamen Nenner finden
🧠 Aufgabenstellung: Bringe die Brüche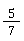 und
und 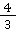 auf einen gemeinsamen Nenner.
auf einen gemeinsamen Nenner.
💡 Anleitung: Wenn du nicht auf Anhieb erkennen kannst, mit welcher Erweiterungszahl du zwei Brüche auf einen Nenner bringst, kannst du sie einfach mit dem Nenner des jeweils anderen Bruchs multiplizieren.
🧮 Rechnung: 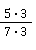 und
und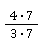
✅ Lösung: 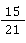 und
und 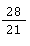 haben den gleichen Nenner 21.
haben den gleichen Nenner 21.
5. Übung: Kleinstes gemeinsames Vielfaches
Zum Abschluss schauen wir uns noch den sogenannten Hauptnenner an. Dieser Hauptnenner ist das kleinste gemeinsame Vielfache von zwei oder mehr ungleichnamigen Brüchen: ⬇️
🧠 Aufgabe: Erweitere die Brüche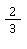 und
und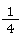 auf ihren Hauptnenner.
auf ihren Hauptnenner.
💡 Anleitung: Notiere dir zuerst alle Vielfachen der beiden Nenner. In unserem Fall sind das die 3er- (weil beim ersten Bruch 3 unter dem Bruchstrich steht) und die 4er-Reihe (weil beim zweiten Bruch 4 unter dem Bruchstrich steht) des kleinen Einmaleins. Für 3 heißt das also: 3, 6, 9, 12, 15 … Und die Vielfachen von 4: 4, 8, 12, 16 … Finde nun die kleinste Zahl, die in beiden Aufzählungen vorkommt! Hast du sie schon entdeckt? 12 kommt in beiden Reihen vor und ist das kleinste gemeinsame Vielfache von 3 und 4. Jetzt musst du nur mehr herausfinden, mit welcher Zahl du die beiden Nenner erweitern musst, damit jeweils 12 herauskommt. Also mit welcher Zahl musst du den Bruch 23 multiplizieren, damit im Nenner 12 steht? Und mit welcher Zahl musst du 14 erweitern, damit unter dem Bruchstrich 12 steht?
🧮 Rechnung: 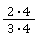 und
und 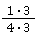
✅ Lösung: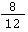 und
und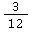 haben den Hauptnenner 12.
haben den Hauptnenner 12.
Du siehst schon: Das Erweitern von Brüchen ist keine Hexerei! Mit ein wenig Übung wirst du ganz schnell zum Rechengenie. Besonderen Spaß macht das Rechnen mit unterhaltsamen Mathe-Apps. Und schmöker doch in unseren Artikel über spielerisches Lernen mit Mathe rein! So bereitet Rechnen sogar kleinen Mathemuffeln Vergnügen! 🤓 💪