Kapitel:
- Subtrahieren von gleichnamigen Brüchen: So geht’s
- Ungleichnamige Brüche subtrahieren
- Brüche subtrahieren: Aufgaben zum Üben
- Bruchrechnen Nachhilfe? Versuch’s mit GoStudent
- Fazit: Brüche subtrahieren kann jeder
Du willst besser verstehen und lernen wie Brüche funktionieren - 💪 aber bist dir beim Subtrahieren unsicher? Dann bist du hier genau richtig! Denn mit ein paar kleinen Kniffen ist das Problem in Windeseile gelöst. Wir zeigen dir hier genau wie es geht. 😇
Also nimm dir ein paar Minuten und lese dir diesen Artikel durch. Am Ende haben wir dir sogar noch ein paar Übungsaufgaben beigefügt. Viel Spaß 🤩
1. Subtrahieren von gleichnamigen Brüchen: So geht’s
Ein Bruch besteht aus drei Teilen: Der Zähler, der sich oben befindet, steht für die Gesamtzahl der Stücke, die gezählt werden. Unten steht ein Nenner, der die vorhandenen Teile des Ganzen beschreibt. Nehmen wir zum Beispiel ein Viertel Pizza, 🍕 das einen Teil einer vierteiligen Pizza bezeichnet. Der Bruchstrich trennt die beiden ganzen Zahlen in der Mitte. Super einfach bis jetzt - oder? 👀
Für Brüche mit demselben Nenner verwenden wir den Ausdruck gleichnamiger Bruch. Hier ist ein Beispiel für einen solchen Bruch:
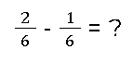
Jetzt musst du nur noch die Zähler subtrahieren: 2 - 1 = 1. Daraus ergibt sich das folgende Ergebnis:
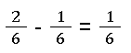
Du brauchst den Nenner nicht zu berechnen, da er bei gleichnamigen Brüchen gleich bleibt. Aber wie sieht das bei gemischten Brüchen aus? Das erklären wir dir im nächsten Absatz ganz einfach und unkompliziert.
Gemischte Brüche subtrahieren
Ein gemischter Bruch ist ein Bruch, dem eine natürliche Zahl vorangestellt ist (1, 2, 3, etc.). Ein Beispiel für einen gemischten Bruch lautet wie folgt:
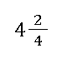
Gemischte Brüche müssen immer zuerst umgerechnet werden. Dazu muss die Multiplikation verwendet werden:
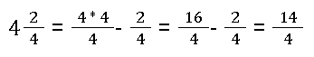
Danach kannst du diese 14 Viertel in 7 Hälften kürzen.
Als Ergebnis können wir nun eine gleichnamige gemischte Bruch-Subtraktion berechnen:
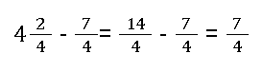
Die Multiplikation von Brüchen sitzt noch nicht ganz? In diesem Artikel haben wir Brüche multiplizieren einfach erklärt.
Brüche mit ganzen Zahlen subtrahieren
Im Gegensatz zu gemischten Brüchen gibt es bei Brüchen mit ganzen Zahlen einen mathematisches Zeichen zwischen der ganzen Zahl und dem Bruch, in diesem Fall ein Minuszeichen bei der Subtraktion. Hier ist ein Beispiel:
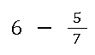
Du kannst diese ganze Zahl einfach in einen Bruch umwandeln. Unabhängig von der Zahl, die davor steht, verwendest du diese Zahl als Zähler und eine 1 als Nenner. Das liegt daran, dass sich eine 4 aus 4 ganzen Zahlen zusammensetzt:
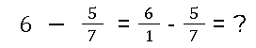
Wie du siehst, ist der Nenner in dieser (und den meisten) Situationen nicht mit dem zweiten Bruch identisch. Folglich musst du den Bruch entweder erweitern oder kürzen. Weiter unten erfährst du mehr über das Subtrahieren von ungleichnamigen Brüchen.
Brüche mit negativen Zahlen subtrahieren
Das Subtrahieren mit negativen, natürlichen Zahlen ist die nächste Stufe (-1, -2, -3, etc.). Wie du schnell feststellen wirst, ist das kein Hexenwerk!
Betrachte das folgende Szenario:
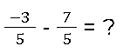
Welche Methode wird hier zum Berechnen verwendet? Wir befinden uns im negativen Bereich der natürlichen Zahlen. Wenn wir -3 mit 7 subtrahieren erhalten wir -10, was ebenfalls eine negative Zahl für den Zähler ist. Daraus ergibt sich folgendes Ergebnis:
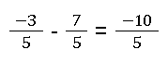
Negative Dezimalzahlen werden auf die gleiche Weise behandelt.
Brüche mit Dezimalzahlen subtrahieren
Was ist die Definition einer Dezimalzahl? Eine Dezimalzahl ist eine natürliche positive oder negative Zahl (1, 2, 3, etc.) auf die weitere Zahlen folgen. Im Folgenden findest du einige Beispiele für Dezimalzahlen:
3,5 oder 4,9 oder 1,2 oder -2,7 usw.
Wie verhält es sich nun, wenn du Brüche mit Dezimalzahlen subtrahierst?
Schauen wir uns das folgende Beispiel an:
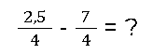
In dieser Situation funktioniert das Subtrahieren genauso wie vorher. Als Ergebnis berechnest du den Zähler also 2,5 - 7 = -4,5. Wir verwenden die folgende Rechenschritte:
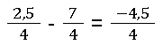
Das funktioniert auch mit negativen ganzen Zahlen, wie wir bereits gezeigt haben. Betrachte die folgende Aufgabe als Beispiel:
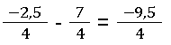
Egal, ob es sich um einen gemischten Bruch oder einen ganzzahligen Bruch handelt, die Technik bleibt dieselbe.
Drei oder mehr Brüche subtrahieren
Nicht alle Aufgaben zur Subtraktion von Brüchen bestehen nur aus zwei Brüchen. Natürlich kannst du auch drei oder mehr Brüche kombinieren. Die Berechnung bleibt jedoch unverändert. Daher führt die folgende Berechnung zu dem vorhergesagten Ergebnis:
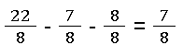
Denn das Ergebnis von 22 - 7 - 8 ist gleich 7.
2. Ungleichnamige Brüche subtrahieren
Bisher haben wir nur Brüche mit demselben Nennern subtrahiert. Wenn die Nenner unterschiedlich sind, bezeichnen wir diese Brüche an ungleichnamig. Betrachte zum Beispiel das Folgende:

Du kannst nicht einfach 5 und 3 addieren, wie es bei einem Bruch mit demselben Nenner möglich ist. Wenn du mit Brüchen mit unterschiedlichen Nennern arbeitest, musst du die Nenner angleichen, bevor du die beiden Brüche addierst.
Dafür gibt es im Wesentlichen zwei Möglichkeiten: Erweitern und Kürzen. Im Folgenden findest du die Erklärungen für beide.
Brüche erweitern
Erweitern ist eine gute Idee, wenn die Nenner klein sind. Große Nenner solltest du hingegen eher kürzen. Betrachte das folgende Beispiel: Wir subtrahieren drei Fünftel von zwei Vierteln.
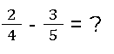
Da die Nenner von 4 und 5 unterschiedlich sind, müssen wir beide Brüche mit einer Zahl multiplizieren, um die Nenner anzugleichen.
Die einfachste Methode dafür, ist das kleinste gemeinsame Vielfache der Nenner zu bestimmen. Bei den Nennern 4 und 5 ist das kleinste gemeinsame Vielfache 20.Die Zahl 20 erhält man, indem man den Multiplikator 4 mit der Zahl 5 multipliziert.
Beim Multiplizieren sollte weder der Nenner noch der Zähler eine Dezimalzahl sein. Versuche stattdessen zu kürzen, wenn das nicht funktioniert. Außerdem kann die Zahl 0 nicht multipliziert werden. Sobald die Nenner gleich sind, wie oben gezeigt, kannst du die Brüche subtrahieren.
Brüche kürzen
Bei größeren Brüchen müssen wir den Prozess umkehren. Du teilst den Zähler und den Nenner durch eine Zahl, die größer ist als 1, um einen Bruch zu kürzen. Das gilt vor allem, wenn es um wirklich große Brüche geht.
Angenommen, du musst die folgenden zwei Brüche addieren:
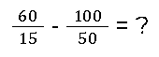
Da die Nenner nicht gleich sind, müssen wir die Nenner angleichen. Erweitern ist eine schlechte Wahl, da du sonst eine Menge Multiplikationen durchführen musst. Deshalb bemühen wir uns, die Zahlen so klein wie möglich zu halten.
So können wir zum Beispiel auf die Zahl 5 kürzen. Der erste Bruch ist durch 3 teilbar, während der zweite Bruch durch 10 teilbar ist. Danach musst du nur noch die beiden ganzen Zahlen addieren oder subtrahieren. Denk daran, dass du nicht durch 0 teilen kannst!
Beim Dividieren dürfen Nenner und Zähler keine ungerade ganze Zahl sein. Wenn das nicht klappt, versuche stattdessen zu erweitern. Du kannst addieren, sobald der Nenner wieder gleich ist, wie du bereits gelernt hast.
3. Brüche subtrahieren: Aufgaben zum Üben
Zu jedem Fall gibt es Übungen und Lösungen. Wir drücken dir die Daumen!
Aufgaben
- Normales Subtrahieren

- Gemischte Brüche subtrahieren
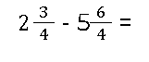
- Brüche mit ganzen Zahlen subtrahieren
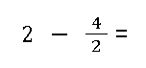
- Brüche mit negativen Zahlen subtrahieren
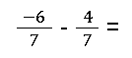
- Brüche mit Dezimalzahlen subtrahieren
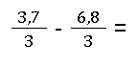
- Drei oder mehr Brüche subtrahieren
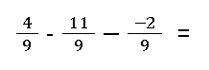
- Brüche erweitern
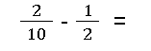
- Brüche kürzen
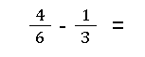
Lösungen
- Normales Subtrahieren
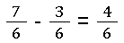
- Gemischte Brüche subtrahieren
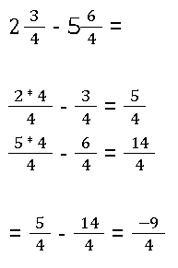
- Brüche mit ganzen Zahlen subtrahieren
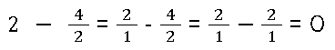
- Brüche mit negativen Zahlen subtrahieren
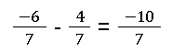
- Brüche mit Dezimalzahlen subtrahieren
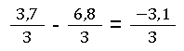
- Drei oder mehr Brüche subtrahieren
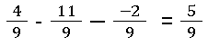
- Brüche erweitern
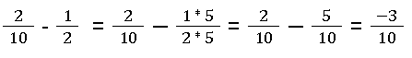
- Brüche kürzen
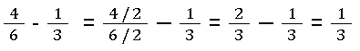
4. Bruchrechnen Nachhilfe? Versuch’s mit GoStudent
5. Fazit: Brüche subtrahieren kannst du lernen
Das Subtrahieren von Brüchen ist ein einfaches Konzept. Wir hoffen, dass dir dieser Artikel beim Verstehen geholfen hat. Jetzt heißt es Üben: Wiederhole die Beispielaufgaben, bis du das Subtrahieren verstanden hast. 👩🏫
Wenn du eine allgemeine Auffrischung zum Thema Brüche brauchst, ist unser Bruchrechnen Einführungsartikel ein guter Anfang. Oder probiere doch mal Quizz oder Apps zum Matheüben!
Und wenn du weitere Fragen hast oder du generelle Probleme mit Mathehast, dann helfen dir unsere GoStudent Nachhilfelehrer gerne weiter. Probiere eine kostenlose Mathe Nachhilfestunde von GoStudent.
Viel Erfolg beim Subtrahieren von Brüchen! 😊