Am Koordinatensystem führt in der Schulzeit für keinen Schüler ein Weg herum. Egal ob für die Grundlagen der Geometrie oder für Gleichungen, mit Koordinatensystemen lassen sich viele verschiedene Phänomene in der Mathematik beschrieben und grafisch darstellen. 😎
Damit auch du verstehst, wie ein Koordinatensystem funktioniert, haben wir hier die wichtigsten Aspekte zusammengefasst. Spannendes Lesen! 🤫
- Was ist ein Koordinatensystem?
- Aufbau eines Koordinatensystems & wie du es zeichnest
- Koordinatensystem Vorlage zum Ausdrucken
Was ist ein Koordinatensystem?
Ein Koordinatensystem ist ein System, umPunkte 📌 in einem Raum zu verorten. Keine Sorge: Das klingt viel komplizierter, als es ist.
Stell dir vor, du stehst in einem Zimmer und möchtest beschreiben, wo du im Raum stehst. 🧐 Zuerst würdest du bestimmt relative Begriffe verwenden, wie zum Beispiel “mittig” oder “am Rand”.
Wenn der Raum aber größer wird, ist die Mitte zum Beispiel sehr unklar. Die Mitte kann auf einem Fußballfeld ⚽️ sehr groß sein, wenn nicht gerade der genaue Mittelpunkt gemeint ist.
Es gibt viele verschiedene Koordinatensysteme, hier zeigen wir dir die wichtigsten Typen.
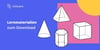
Der Zahlenstrahl / die Zahlengerade
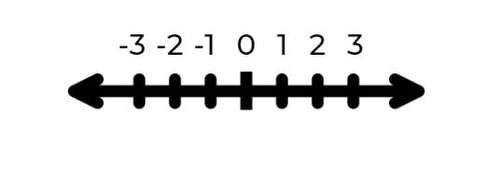
Der Zahlenstrahl ist im Prinzip eine Linie, 📏 die verwendet wird, um reelle Zahlen der Reihe nach zu ordnen. Reelle Zahlen sind in der Mathematik alle natürlichen Zahlen (1, 2, 3 etc.), alle ganzen Zahlen (also auch negative Zahlen) sowie Brüche, allerdings keine Dezimalzahlen (Zahlen mit Komma).
Beim Zahlenstrahl geht es nun darum, die unendliche Reihenfolge von Zahlen zu veranschaulichen. Der Zahlenstrahl kann sowohl positiv als auch negativ unendlich weit fortgeführt werden. Außerdem verdeutlicht er, wie die Abstände zwischen den einzelnen Zahlen aussehen. Er ermöglicht besonders jüngeren Kindern, die Bedeutung und Rolle von Zahlen genauer zu verstehen. 🔮
Das kartesische zweidimensionale Koordinatensystem
Wenn der Begriff Kartesisches Koordinatensystem fällt, ist meistens ein zweidimensionales Koordinatensystem gemeint. Das bedeutet, es zeigt eine Fläche an. Egal ob es sich um Meeresoberflächen 🌊 oder Stoffbahnen handelt, mit dem Koordinatensystem bekommt jeder Punkt im Raum eine Bezeichnung.
Im nächsten Kapitel gehen wir darauf ein, wie du dieses Koordinatensystem zeichnen kannst und aus welchen Bestandteilen es besteht. Aber zuerst stellen wir noch ein paar weitere Koordinatensysteme vor.
Das kartesische dreidimensionale Koordinatensystem
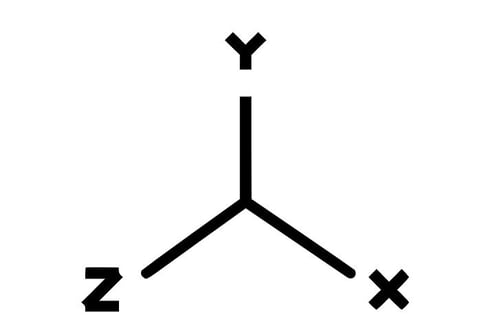
Als logische Fortsetzung des zweidimensionalen Koordinatensystems bekommt das kartesische nun 3 Dimensionen. 🎲 Wenn du dir einen Raum vorstellst, kannst du nun nicht nur beschreiben, wo auf dem Boden jemand steht. Du könntest zum Beispiel auch sagen, auf welcher Höhe sich der Kopf einer Person befindet. 🤓
Mit der Angabe des zweidimensionalen Punktes auf der Fläche und der dritten Dimension in der Höhe gibt es nun auch für den Kopf eine klare Ortsangabe.
Dieses Koordinatensystem ist besonders wichtig, um räumliche Körper beschreiben und veranschaulichen zu können. 🟢
Das Polarkoordinatensystem
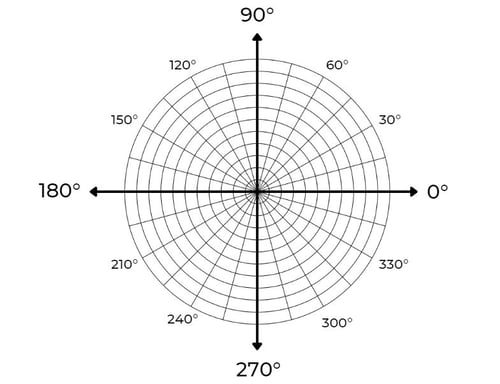
Bei rechteckigen Flächen funktionieren Koordinatensysteme besonders einfach. Allerdings sind viele Flächen und Körper nicht unbedingt so einfach – angefangen bei unserer schönen, runden Erde. 🌐
Aus diesem Grund wurde das Polarkoordinatensystem erfunden. Dieses gibt es nur in der Ebene, also zweidimensional, es gibt hier nicht drei oder vier Dimensionen. Allerdings ist die Verwendung dieses Koordinatensystems deutlich schwieriger und komplexer und für den Matheunterricht in der Regel nicht nötig, daher werden wir hier nicht weiter darauf eingehen. 🌍
Aufbau eines Koordinatensystems & wie du es zeichnest
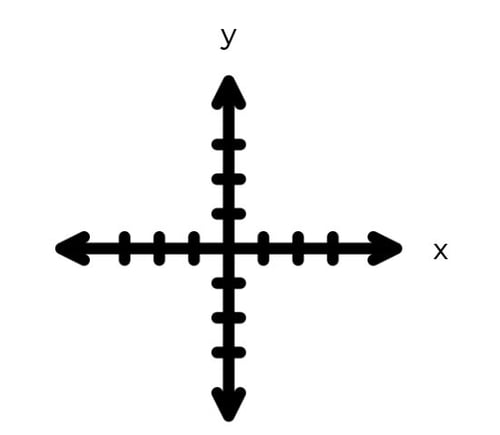
Das klassische, zweidimensionale kartesische Koordinatensystem besteht aus zwei Achsen, die im rechten Winkel zueinander stehen, der senkrechten y-Achse und der waagerechten x-Achse. 📐
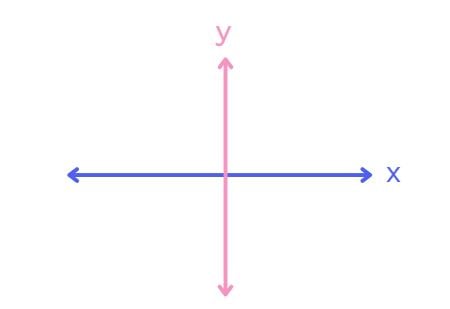
Die y-Achse wird auch als Ordinate bezeichnet, während die x-Achse auch Abszisse genannt wird. Dort, wo sich Ordinate und Abszisse kreuzen, liegt der sogenannte Ursprung. Dort ist der Zahlenwert von X und Y = 0. 0️⃣
Quadranten des Koordinatensystems
Das Koordinatensystem kann auch als Kreuz dargestellt werden, so können beide Achsen (die im Prinzip Zahlengeraden sind), auch negative Zahlen darstellen. Die 4 Bereiche dieses Koordinatensystems nennen wir von oben links ausgehend entgegen dem Uhrzeigersinn Quadranten:
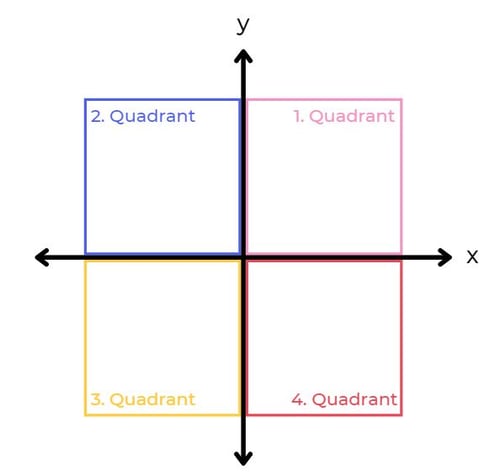
- Oben Rechts - 1. Quadrant 1️⃣
- Oben Links - 2. Quadrant 2️⃣
- Unten Links - 3. Quadrant 3️⃣
- Unten Rechts - 4. Quadrant 4️⃣
Achsen und Punkte im Koordinatensystem
Wie werden hier nun Punkte benannt? Dafür müssen wir zuerst die Achsen beschriften.
Wenn du ein Koordinatensystem auf einem karierten Papier zeichnest, kannst du einfach pro Karo die Achsen benennen. Die erste Zahl auf der X-Achse nach rechts gehend nennen wir 1. Dafür musst du lediglich einen Strich ziehen und eine 1 darunter schreiben. Darauf folgt 2 und 3 und so weiter. 🤠
Das gleich machen wir mit der Y-Achse. Vergiss auch bitte nicht, beide Achsen mit einem Pfeil zu beenden. So zeigst du, dass du weißt, dass die Zahlen bis ins Unendliche hinein fortgesetzt werden können. Gerade für Mathe-Prüfungen oder gar das Mathe-Abitur ist das wichtig.
Im nächsten Schritt können wir nun endlich einen Punkt benennen. 🤗
Nehmen wir nun an, dass du einen Punkt dort im Koordinatensystem einzeichnest, wo die X-Achse und die Y-Achse beide bei 1 liegen. Diesen Punkt können wir nun folgendermaßen bezeichnen:
P (1 | 1)
Diese Notierung bedeutet, dass der Punkt (P) auf der X-Achse bei 1 und auf der Y-Achse bei 1 liegt. Merke, das X kommt immer zuerst, wie auch im Alphabet. 🔡
Würden wir dagegen den Punkt P (3 | 2) haben, dann würde der bei der X-Achse auf 3 und bei der Y-Achse auf 2 liegen. So einfach geht das!
Genauso kannst du negative Punkte einzeichnen. Nimm zum Beispiel den Punkt P (-4 | 3). Dieser liegt im 2. Quadranten. Denn er ist auf der X-Achse im negativen (linken) Bereich und bleibt bei der Y-Achse im positiven (oberen Bereich).
Dreiecke im Koordinatensystem
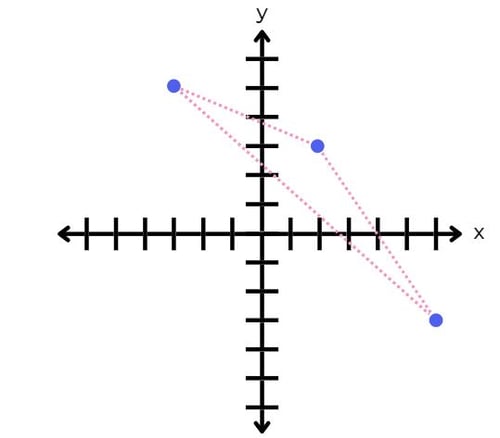
Wir können nun auch geometrische Strukturen im Koordinatensystem darstellen. Wie würdest du ein Dreieck zeichnen? 🔻
Ganz einfach: Erstelle zuerst eine Gerade. Dafür musst du nur zwei Punkte einzeichnen, zum Beispiel P (2 | 3) und P (-3 | 5), und diese dann mit einer Gerade verbinden. Füge dann noch einen dritten Punkt hinzu, P (6 | -3) – und fertig ist das Dreieck!
Dreidimensionales Koordinatensystem
Wie sehen nun dreidimensionale Koordinatensysteme aus? Zeichne zuerst den 1. Quadranten. Danach ziehe eine dritte Achse nach schräg unten.

Wenn du jetzt Punkte einzeichnest, dann entsteht ein dreidimensionaler Körper. Das kann schnell verwirrend werden, aber keine Sorge – in der Schule wird es nicht sehr umfangreich behandelt. 🧠
Koordinatensystem Vorlage zum Ausdrucken
Herzlichen Glückwunsch, du hast es bis zum Ende geschafft! Jetzt hast du genau verstanden, was ein Koordinatensystem ist, welche Typen es gibt und wie du ein Koordinatensystem erstellst. 😇
Du brauchst noch weitere Hilfe mit Koordinatensystemen und Mathematik? Probiere doch einfach kostenlos unsere Mathe Nachhilfe aus! Melde dich einfach für eine Probestunde ohne weitere Verpflichtungen an. Danach wird sich einer unserer freundlichen Mitarbeiter persönlich bei dir melden und alles weitere besprechen!
Damit du auch zu Hause noch alle Materialien beisammen hast, kannst du hier gerne die wichtigsten Koordinatensysteme ausdrucken: