Kapitel:
- Quadratische Ergänzung: Einfach erklärt
- Von der Quadratischen Ergänzung zu den Scheitelpunkten
- Der Hintergrund der Quadratischen Ergänzung
- Quadratische Ergänzung üben mit unseren Aufgaben & Übungen
Mit der quadratischen Ergänzung kannst du eine Quadratische Gleichung in ein Binom umformen. 🤓 Keine Angst, selbst wenn du keinen dieser Begriffe kennst, zeigen wir dir einfach und unkompliziert, was das bedeutet und wie das geht. Viel Erfolg! 🤠
1. Quadratische Ergänzung: Einfach erklärt
Wir beginnen mit einer Quadratischen Gleichung in der Allgemeinen Form ax2 + bx + c = 0. Nehmen wir zum Beispiel die folgende:
2x2 + 8x - 10 = 0.
Von dort möchten wir hierher kommen, also zu einem quadrierten Binom (in Klammern).
2(x + 22) - 18 = 0.
Für die Umformung brauchst du die erste oder zweite Binomische Formel. ✅ Hier zeigen wir dir, wie das geht:
1. Vor dem Term x2 in der Allgemeinen Form ist ein Faktor (2), den wir ausklammern wollen.
2(x2 + 4x) - 10 = 0.
2. Als nächstes wollen wir den Faktor 4 durch 2 dividieren und dann quadrieren, also 4/2 = 2 und 22 = 4.. Diese 4 können wir jetzt zum Term in der Klammer addieren und direkt wieder subtrahieren, was keine Änderung des Term-Inhaltes bedeutet. Klingt unnötig? 🧐 Lies weiter!
2(x2 + 4x + 4 - 4) - 10 = 0
3. Wie du merkst, kannst du jetzt mit der ersten binomischen Formel weitermachen.
2(x2 + 4x + 4 - 4) - 10 = 0.
= 2((x + 2)2 - 4) - 10
= 2(x + 2)2 - 8 - 10
= 2(x + 2)2 - 18
Welcher Schritt davon war die Quadratische Ergänzung? In Schritt 2 hast du die quadrierte Hälfte der Zahl vor dem x einmal addiert und einmal subtrahiert. Dadurch konntest du die binomische Formel anwenden. Und dieser Teil ist die eigentliche Quadratische Ergänzung und nennt sich auch Nullergänzung. 👻
Jetzt stellst du dir natürlich die Frage, wofür die ganze Umformung überhaupt nutzt. Generell kannst du die Gleichung nun mit der PQ-Formel auflösen. Das geht allerdings auch schon vor der Quadratischen Ergänzung.
Der Hauptgrund ist tatsächlich, dass du von hier aus den Scheitelpunkt berechnen kannst. Wir zeigen dir, wie das geht. 🤗
2. Von der Quadratischen Ergänzung zu den Scheitelpunkten
Um den Scheitelpunkt einer Quadratischen Gleichung zu berechnen wird meist die Quadratische Ergänzung verwendet. Aber was ist ein Scheitelpunkt? 🤔
Anders als bei einer linearen Gleichung können wir den Graphen einer Quadratischen Gleichung nicht als Gerade sondern als Parabel beschreiben.
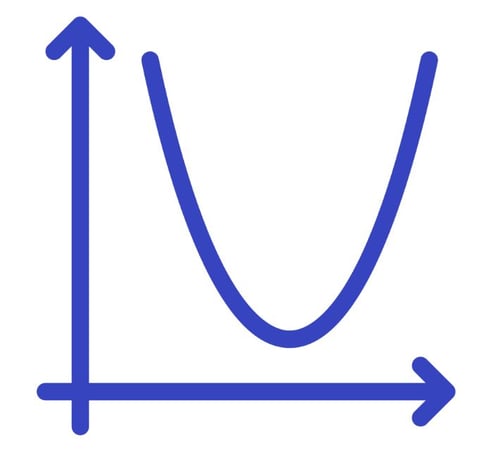
Bei einer Quadratischen Gleichung bezeichnen wir den höchsten oder niedrigsten Punkt der Parabel als Scheitelpunkt.
Wenn die Parabel nach unten hin geöffnet ist, dann ist der Scheitelpunkt der höchste Punkt im Koordinatensystem. Ist die Parabel hingegen nach oben hin geöffnet, ist er natürlich der niedrigste Punkt. Entsprechend spricht man auch vom Minimum oder Maximum einer Quadratischen Gleichung.
Diesen Scheitelpunkt kann man aus der sogenannten Scheitelpunktform herauslesen. Diese sieht so aus:
f(x) = a(x - d2) + e
Dabei sind d und e die Koordinaten des Scheitelpunktes. Dies wird auch so geschrieben S (d | e).
Die Scheitelpunktform erinnert dich an etwas? Richtig, ✅ du kannst sie nämlich mit der Quadratischen Ergänzung herleiten.
Nehmen wir dafür einmal die Funktion f(x) = - x2 + 4x + 4
Wir ergänzen im nächsten Schritt den quadratischen Term mit der Nullergänzung:
- x2 + 4x + 4
= - (x2 - 4x) + 4
= - (x2 - 4x + 4 - 4) + 4
= - ((x - 2x2)- 4) + 4
= - (x - 22) + 8
Hier erkennst du die Scheitelpunktform wieder, die wir oben vorgestellt haben: 👀
- (x - 22) + 8
Die Koordinaten des Scheitelpunktes sind also S (2 | 8).
Du siehst auch, dass die Parabel nach unten hin geöffnet ist, denn der Faktor davor ist ein Minus.
3. Der Hintergrund der Quadratischen Ergänzung
Eine Quadratische Gleichung ist eine Gleichung mit einer quadrierten Unbekannten 👨🎤 (z.B. x2):
4x2 + 2x + 3 = 0
Die Quadratische Gleichung kann man in verschiedenen, sogenannten Formen aufschreiben. Das obige Beispiel ist zum Beispiel die Allgemeine Form. Sie enthält die drei Koeffizienten einer quadratischen Gleichung - a als quadratisches Glied, b als lineares Glied und c als konstantes Glied:
Allgemeine Form: ax2 + bx + c = 0
Formen ändern nichts am Inhalt der Gleichung. Sie sehen nur anders aus, weil wir damit verschiedene Operationen durchführen können. Außerdem gibt es die Normalform:
Normalform: x2 + px + q = 0
In die Normalform oder die Allgemeine Form kommt man meist durch Umformung ausgehend von einer einfachen Quadratischen Gleichung. Von der Normalform aus kannst du die Quadratische Gleichung mit der sogenannten PQ-Formel lösen.
Wie kommt jetzt die Quadratische Ergänzung ins Spiel? 🤷♂️
Sie wird bei einer Quadratischen Gleichung in Allgemeiner Form verwendet, um ein Quadriertes Binom zu bekommen. Der Begriff Binom kommt von den Drei Binomischen Formeln. Diese bauen auf den Prinzipien Punkt-vor-Strich und Ausklammern auf und sind Standardbeispiele für die Verrechnung von zwei oder mehr Binomen, z.B. (a+b) x (a+b). Damit sind sie für die Umformung von Gleichungen super wichtig.
4. Quadratische Ergänzung üben mit unseren Aufgaben & Übungen
Damit du die Quadratische Ergänzung auch zusätzlich zu Hause 🏡 lernen und vertiefen kannst, haben wir dir ein paar Übungsaufgaben mitgegeben. Diese findest du hier:
Aufgaben:
3 x2 + 6 x + 3 =
4 x2 + 4 x + 4 =
2 x2 + 8 x + 5 =
6 x2 + 3 x + 4 =
2 x2 − 4 x =
0,5 x2 − 2 x + 4 =
Lösungen:
3x2+6x+3
3(x2+2x)+3
3(x2+2x+12-12)+3
3((x+1)2-1)+3
3(x+1)2-3+3
3(x+1)2
4x2+4x+4
4(x2+x)+4
4(x2+x+0,52-0,52)+4
4((x+0,5)2-0,25)+4
4(x+0,5)2-1+4
4(x+0,5)2+3
2x2+8x+5
2(x2+4x)+5
2(x2+4x+22-22)+5
2((x+2)2-4)+5
2(x+2)2-8+5
2(x+2)2-3
6x2+3x+4
6(x2+0,5x)+4
6(x2+0,5x+0,252-0,252)+4
6((x+0,25)2-0,0625)+4
6(x+0,25)2-0,375+4
6(x+0,25)2+3,625
2x2−4x
2(x2-2x)
2(x2-2x+1-1)
2((x-1)2-1)
2(x-1)2-2)
0,5x2−2x+4
0,5(x2-4x) + 4
0,5(x2-4x + 4-4) + 4
0,5((x-2x) 2-4) + 4
0,5(x-2)2 + 2