Dreisatz einfach erklärt: Formel & Übungsaufgaben

Kapitel:

1. Der Dreisatz einfach erklärt
2. Proportionaler Dreisatz 
3. Antiproportionaler Dreisatz
4. Doppelter Dreisatz, Dreifacher Dreisatz und Zusammengesetzter Dreisatz (Kettensatz)
5. 3 Tipps bei Dreisatzaufgaben
6. Dreisatz Aufgaben zum Üben

Wenn es eine Sache gibt, die du unbedingt aus der Mathematik mitnehmen solltest, dann ist es das Prinzip des Dreisatzes. Denn der Dreisatz kann auch für den Alltag sehr nützlich sein. 🤠

Wir zeigen dir kurz und knapp, was der Dreisatz ist und wie du ihn anwendest. 😇 Am Schluss gibt’s auch noch Übungsaufgaben mit Lösungen. Viel Erfolg!

Der Dreisatz einfach erklärt

Das Grundprinzip des Dreisatzes ist, dass wir 2 Größen haben, die miteinander in Beziehung stehen. ⚖️ In 3 Schritten (daher der Name Dreisatz), können wir das Ergebnis ausrechnen.

Was bedeutet das im Detail? Hier zwei Beispielfragen:

1. Wenn ein Auto 🚗 in 3 Stunden 120 Kilometer zurücklegt, wie weit fährt es dann in 5 Stunden?
2. Du hast ein Pizza-Rezept 🍕 für 2 Personen. Wie ändert sich die Menge der Zutaten, wenn du für 3 Personen backen möchtest?

Beim Dreisatz geht es nicht um komplizierte Mathematik, sondern darum, aus praktischen Sachverhalten herauszulesen, wie die Lösung zu finden ist - denn die Lösung funktioniert immer nach den gleichen Prinzipien. Die einzige Mathematik, die du dafür brauchst, ist die grundlegende Multiplikation ✖️ und Division, ➗ mehr nicht. 

Das heißt, der Dreisatz ist eine praktische Sache mit echtem Realitätsbezug und kann täglich angewendet werden - und daher solltest du ihn auch können. Jetzt aber rein ins Thema! 😜

Proportionaler Dreisatz

Der proportionale Dreisatz wird auch der klassische oder typische Dreisatz genannt. Der Name kommt daher, dass die beiden Bezugsgrößen proportional miteinander ansteigen. 

Zum Beispiel: Je mehr Eier du kaufst, desto mehr Geld wirst du ausgeben. 💰 Drei Folgen deiner Lieblingsserie dauern insgesamt 95 Minuten. Wie lange dauern fünf Folgen?

Wie der Dreisatz sagt, finden wir die Lösung in drei Schritten. 

Fragestellung: 100 Gramm Käse 🧀 kosten 0,9 Euro. Wie viel kosten 3 Kilo Käse?

Schritt 1: Erfasse die Daten

• 0,1 Kilo Käse kosten 0,9 Euro
• Du suchst nach dem Preis für 3 Kilo Käse. 

Es geht also um den Preis in Beziehung zum Gewicht. Du weißt das Gewicht bei beiden Fällen, aber den Preis nur bei einem. 

Schritt 2: Berechne den Standardpreis (Preis für 1 Kilo Käse)

• 1 Kilo sind 10 x 100 Gramm also 1000 Gramm.
• Also kostet ein Kilo Käse 10 x 0,9 Euro = 9 Euro

1 Kilo Käse (der Standardpreis) kostet 9 Euro.

Schritt 3: Berechne die Lösung mit dem Standardpreis

• Wenn 1 Kilo Käse 9 Euro kosten, dann kostet 3 Kilo Käse 3 x 9 Euro = 27 Euro.

Das ganze kannst du auch in einer Formel betrachten:

Oder, mit den präzisen Angaben, die hier relevant sind:

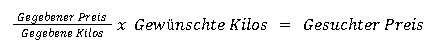
Wie du bereits merkst, ist der entscheidende Schritt hier, die verschiedenen Größen mental zuzuordnen. Was ist die gegebene Größe und Menge? Was ist gesucht?

Danach musst du einfach nur die Schritte durchführen wie hier gelernt. 

Antiproportionaler Dreisatz

Der unproportionale Dreisatz funktioniert im Prinzip wie der proportionale. Allerdings sind die Bezugsgrößen unproportional im Verhältnis miteinander. Er wird daher auch umgekehrter Dreisatz genannt. 🔄

Beispiel: 8 Helfer sollten dir bei deinem Umzug helfen. 🚛 Gemeinsam würden sie dann je 16 Kisten tragen müssen. Leider fallen 4 Helfer aus, sodass nur noch 4 insgesamt übrig bleiben. Wie viele Kisten muss jeder einzelne von ihnen nun tragen?

Auch hier finden wir die Lösung wieder in 3 Schritten.

Fragestellung: Wie viele Kisten muss jeder einzelne der 4 Helfer tragen?

Schritt 1: Erfasse die Daten

• 8 Helfer sollten 16 Kisten tragen. 
• Du suchst nach der Anzahl Kisten pro Helfer.

Hier geht es um die Anzahl Kisten pro Helfer. Du weißt die Anzahl Helfer in beiden Fällen, aber nicht die Anzahl der Kisten im zweiten Fall.

Schritt 2: Berechne die Gesamtzahl der Kisten 

• Es gab 8 Helfer, die je 16 Kisten tragen sollten. 
• Also gibt es insgesamt 8 x 16 = 128 Kisten

Wir müssen also herausfinden, wie sich diese 128 Kisten auf die tatsächlichen 4 Helfer verteilen.

Schritt 3: Berechne die Anzahl der Kisten pro 4 Helfer

• Da es nur 4 Helfer gibt, teilen wir 128 Kisten durch 4 Helfer, also 128 / 4 = 32
• Also muss jeder der 4 Helfer 32 Kisten schleppen - die Armen! 😥

Natürlich lässt sich auch das wieder in einer Formel darstellen:

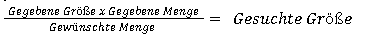
Also mit unseren Angaben

Doppelter Dreisatz, Dreifacher Dreisatz und Zusammengesetzter Dreisatz (Kettensatz)

Diese Art von Verhältnis-Aufgaben lässt sich natürlich noch ein bisschen komplizierter gestalten. Bis jetzt hatten wir 2 Bezugsgrößen in einem Verhältnis miteinander. Das ganze geht aber auch mit 3 oder mehreren Bezugsgrößen und sowohl im proportionalen als auch antiproportionalen Verhältnis. 

Man spricht dann vom doppelten oder dreifachen Dreisatz sowie vom Zusammengesetzten Dreisatz (auch Kettensatz genannt).

Natürlich rechnen wir auch hier mit dir ein Beispiel durch.

Wenn 7 Fliesenleger 👷‍♀️ für 720 m² 160 Stunden brauchen (pro Person, also wenn alle parallel arbeiten), wie lange bräuchten dann 5 Fliesenleger für eine Fläche von 600 m²?

Fragestellung: Wie viele Quadratmeter (m²) Fliesen kann ein Fliesenleger in einer Stunde legen? Und wie lange brauchen dann 5 Fliesenleger für 600 m²?

Schritt 1: Erfasse die Daten

• 7 Fliesenleger brauchen 160 Stunden für 720m²
• Wir wollen wissen, wie viele Quadratmeter ein Fliesenleger in einer Stunde  legen kann.

Hier kannst du sowohl rechnen, wie viele Quadratmeter ein Fliesenleger pro Stunde schafft, als auch wie viel Zeit ein Fliesenleger für einen Quadratmeter Fliesen braucht. Du musst allerdings konsistent in den weiteren Schritten bleiben!

Schritt 2: Berechne die Fläche pro Zeit (Quadratmeter pro Zeit)

• Wie viele Quadratmeter werden von 7 Fliesenlegern in einer Stunde ⏰ gelegt? 720 m² / 160h = 4,5 m²
• Wie viele Quadratmeter schafft also einer von 7 Fliesenlegern pro Stunde? 4,5 m² / 7 Fliesenleger = 0,64 m² pro Stunde pro Fliesenleger. 

Wir wissen nun, wie viel Fläche pro Stunde ein Fliesenleger schafft. Also können wir berechnen, wie lange 5 Fliesenleger für 600 m²  benötigen.

Schritt 3: Berechne die Anzahl Stunden für die gesuchte Fläche

• Wir haben 5 Fliesenleger für 600 m². Ein Fliesenleger schafft in einer Stunde 0,64 m².
• 600 m² bedeutet 600 / 5 = 120 m² für jeden der 5 Fliesenleger. 
• 120 m² / 0,64 m² pro Stunde = 187,5 Stunden pro Fliesenleger. 

Die Antwort ist also, dass 5 Fliesenleger 187,5 Stunden arbeiten müssen (pro Person, wenn alle parallel arbeiten), um eine Fläche von 600 m² zu legen. 

3 Tipps bei Dreisatzaufgaben

1. Schaue dir die die Aufgabenstellung genau an

Es kann manchmal sein, dass die Aufgabenstellungen beim Dreisatz extremst kompliziert wirken. 🚫 Dabei ist dieses Thema in der Mathematik eigentlich eines der einfachsten. Lass dich also nicht aus der Ruhe bringen. Schaue dir genau an, wonach gefragt ist und welche Bezugsgrößen miteinander im Verhältnis liegen. 🧐

2. Es wird nach einer einzigen Sache gesucht.

Bei einigen Aufgabenstellungen sieht es auf den ersten Blick so aus, als ob nach einer bestimmten Lösung gesucht wird. 🤔 Schaue aber trotzdem ein zweites Mal hin, ob es nicht doch eine andere Größe ist. Vergiss außerdem nicht, dass es niemals zwei Dinge gibt, wonach gesucht wird. Das Verhältnis des Gesuchten zu den bereits existierenden Größen sollte außerdem über alle drei Rechenschritte genau gleich sein. 

3. Schreibe deinen Denk- und Rechenweg auf

Egal wie einfach es aussieht - mit Stift 🖍 und Papier hast du die beste Gedankenstütze. Schreibe dir immer auf, welche Informationen du bereits hast und wonach gesucht wird. Du kannst dir auch eine Tabelle erstellen, um schrittweise durch alle drei Rechenschritte zu gehen. Vergiss am Ende auch nicht, noch einmal drüber zu schauen, damit du nichts vergessen und dich nirgendwo verrechnet hast. 🤓

Dreisatz Aufgaben zum Üben

Dreisatz ist nicht schwer - das hast du jetzt bestimmt schon lange gemerkt. Es ist aber trotzdem eine Übungssache. Wenn du Hilfe beim Dreisatz brauchst, dann probiere doch unsere kostenlose Mathe-Nachhilfestunde aus und teste GoStudent Nachhilfe.

Und weil Übung ja bekanntlich den Meister macht, haben wir dir ein paar Übungen zusammengestellt. Damit kannst du zu Hause noch einmal über das Thema drüber gehen und sie alleine suchen. Natürlich haben wir dir auch die Lösungen dazu gegeben. Viel Erfolg!

Fragen:

1. Auf einem Bauernhof gibt es Kühe, die gemeinsam jede zwei Tage insgesamt 400 Liter Milch geben. Der Besitzer der Kühe wird gefragt, ob er innerhalb von sieben Tagen 1.500 Liter produzieren kann. Ist das möglich?
2. Drei Strohbälle haben ein Gewicht von 1,5 Tonnen. Wie viel wiegen fünf Strohballen?
3. Es sollen Steine mit Lastwagen transportiert werden. Drei LKWs schaffen die Arbeit in 21 Stunden. Wie lange würde es mit sieben LKWs dauern?
4. Max bringt Pfandflaschen in den Supermarkt. Für 12 Flaschen bekommt er 1,8 Euro. Wie viel bekäme er für 87 Flaschen? 
5. Frau Schmidt fährt Cabrio. Für eine Strecke von 68 Km Länge benötigt das Auto 2,72 Liter Benzin. Wie viel würde es bei 13 Km benötigen? 
6. In 5 Kellern findest du 40 Ratten. Wie viele würdest du in 13 Kellern finden?
7. Nach einer großen Hochzeit brauchen 6 Personen genau 3 Stunden und 15 Minuten zum Aufräumen des Saals. Wie viele Menschen könnten das in 30 Minuten schaffen?
8. Die alte Bücherei in der Schule hat 5 Regale die jeweils 7 Reihen haben. In 4 Reihen gibt es 56 Schulbücher. Wie viele Bücher findest du in 4 Regalen?

Lösungen:

1. Auf einem Bauernhof gibt es Kühe, die gemeinsam jede zwei Tage insgesamt 400 Liter Milch geben. Der Besitzer der Kühe wird gefragt, ob er innerhalb von sieben Tagen 1.500 Liter produzieren kann. Ist das möglich?
2. Antwort: Nein, er kann maximal 1.400 Liter in sieben Tagen produzieren.
3. Drei Strohbälle haben ein Gewicht von 1,5 Tonnen. Wie viel wiegen fünf Strohballen?
4. Antwort: Fünf Strohballen wiegen 2,5 Tonnen. 
5. Es sollen Steine mit Lastwagen transportiert werden. Drei LKWs schaffen die Arbeit in 21 Stunden. Wie lange würde es mit sieben LKWs dauern?
6. Antwort: Sieben Lastwagen würden genau 9 Stunden benötigen. 
7. Max bringt Pfandflaschen in den Supermarkt. Für 12 Flaschen bekommt er 1,8 Euro. Wie viel bekäme er für 87 Flaschen? 
8. Antwort: Er bekäme 13,05 Euro.
9. Frau Schmidt fährt Cabrio. Für eine Strecke von 68 Km Länge benötigt das Auto 2,72 Liter Benzin. Wie viel würde es bei 13 Km benötigen? 
10. Antwort: Das Auto würde 0,52 Liter benötigen.
11. In 5 Kellern findest du 40 Ratten. Wie viele würdest du in 13 Kellern finden?
12. Antwort: Du würdest 104 Ratten finden.
13. Nach einer großen Hochzeit brauchen 6 Personen genau 3 Stunden und 15 Minuten zum Aufräumen des Saals. Wie viele Menschen könnten das in 30 Minuten schaffen?
14. Antwort: 39 Personen könnten es schaffen. 
15. Die alte Bücherei in der Schule hat 5 Regale die jeweils 7 Reihen haben. In 4 Reihen gibt es 56 Schulbücher. Wie viele Bücher findest du in 4 Regalen?
16. Antwort: Du findest 392 Bücher.