Kapitel:
- Brüche dividieren einfach erklärt
- Brüche kürzen
- Brüche dividieren: Beispiele, Aufgaben & Übungen
- Fazit: Brüche multiplizieren ist einfach, wenn gewusst wie
In diesem Artikel zeigen wir dir alles, was du über das Brüche Dividieren wissen musst. Am Ende findest du außerdem Übungsbeispiele mit Lösungen. So schaffst du den nächsten Mathe-Test bestimmt!
Du willst ganz von vorne beginnen? Dann lese dir hier die Grundlagen der Bruchrechnung durch.
1. Brüche Dividieren einfach erklärt
Es gibt eine einfache Methode, um Brüche zu dividieren. Dabei spiel überhaupt keine Rolle, ob der Zähler und der Nenner gleich sind. Du musst dafür nicht mal erweitern oder kürzen.
Hier ist ein Beispiel für eine Division:
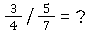
Um diese beiden Brüche zu dividieren, musst du den zweiten Bruch zuerst einmal umstellen. Das nennt sich der Kehrwert. 🔄 Fünf Siebtel wird also zu sieben Fünftel:
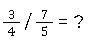
Danach multiplizierst du einfach ihre jeweiligen Nenner und Zähler.
Als Ergebnis kommt Folgendes heraus:
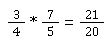
Dividieren von gemischten Brüchen
Wie sieht es bei gemischten Brüchen aus? Bei gemischten Brüchen steht eine natürliche Zahl vor dem realen Bruch.
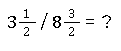
Bevor du dividieren kannst, müssen die gemischten Brüche erst einmal umgewandelt werden:
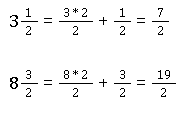
Im nächsten Schritt musst du beide miteinander multiplizieren. Aber, wie oben bereits erklärt, musst du dafür den zweiten Bruch umstellen:
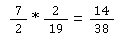
Dividieren mit negativen Zahlen
Als Faustregel gelten die Vorzeichenregeln für die Division von positiven und negativen ganzen Zahlen. Das ist nötig, wenn mit negativen Zahlen dividiert wird.
- Plus und Plus bleibt Plus
- Plus und Minus wird Minus
- Minus und Plus wird Minus
- Minus und Minus ergibt Plus
Wie lautet also die Lösung der folgenden Aufgabe?
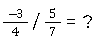
Wie oben bereits gelernt, musst du den zweiten Bruch umstellen. Die Aufgabe lautet dann also:
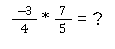
Folglich ist das Endprodukt:
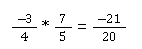
Dividieren mit Dezimalzahlen
Auch die Division von Dezimalzahlen mit Brüchen ist ganz einfach. 2,4 oder 5,7 sind Beispiele für dezimale ganze Zahlen mit Nachkommastellen.
Wie wir bereits gelernt haben, ist die Berechnung ganz einfach:
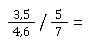
Mit Umstellung ergibt sich:
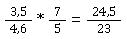
Negative oder gemischte Zahlen ändern auch nichts an der Vorgehensweise.
Dividieren mit drei oder mehr Brüchen
Jetzt fügen wir noch eine weitere Ebene hinzu, um die Komplexität zu erhöhen! Anstelle von zwei Brüchen arbeiten wir jetzt mit drei.
Zum Beispiel:
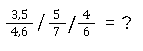
In diesem Fall werden der zweite und der dritte Bruch umgedreht:
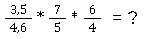
Im Anschluss musst du nur noch die Multiplikation durchführen - kinderleicht!
2. Brüche kürzen
Die Erweiterung oder Kürzung von Brüchen ist möglich, wenn die Nenner der Brüche bei Addition und Subtraktion nicht gleich sind. Die Erweiterung wird verwendet, wenn die Zähler kleiner als die Nenner sind.
Wenn du einen Bruch kürzen willst, musst du Zähler und Nenner mit einem Wert größer als 1 teilen. Besonders bei großen Brüchen kürzen wir.
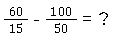
Wir können zum Beispiel bis auf 5 kürzen. Dafür werden Zähler und Nenner des ersten Bruches durch 3 und des zweiten Bruches durch 10 dividiert. Das Addieren oder Subtrahieren der beiden Ergebnisse ist alles, was übrig bleibt. Denke daran, dass du nicht durch 0 dividieren kannst!
Bei der Division dürfen Zähler und Nenner keine ungeraden Zahlen sein. Es kann sein, dass das nicht funktioniert, aber das Erweitern schon. Wenn der Nenner wieder gleich ist, kannst du addieren oder subtrahieren, wie du es vorher gelernt hast.
3. Brüche dividieren: Beispiele, Aufgaben & Übungen
Wir wollen, dass du das Gelernte auch anwenden kannst. Daher haben wir zuerst hier noch einmal ein paar Beispielaufgaben für jede Divisions-Art aufgelistet. Unterhalb findest du die Lösungen.
Brüche dividieren Aufgaben
Normales Dividieren
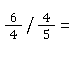
Dividieren mit gemischten Brüchen
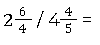
Dividieren mit negativen Zahlen
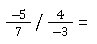
Dividieren mit Dezimalzahlen
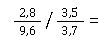
Dividieren mit drei oder mehr Brüchen
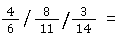
Dividieren mit gemischten Operationen
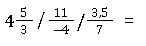
Wir berechnen zuerst den gemischten Bruch
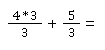
Und dann den Rest
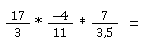
Lösungen
Normales Dividieren
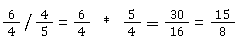
Dividieren mit gemischten Brüchen
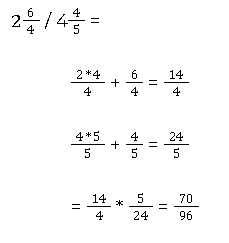
Dividieren mit negativen Zahlen
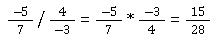
Dividieren mit Dezimalzahlen
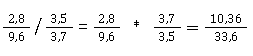
Dividieren mit drei oder mehr Brüchen
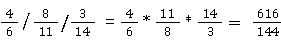
Dividieren mit gemischten Operationen
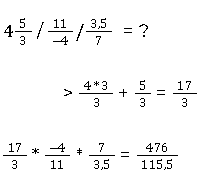
Wir berechnen zuerst den gemischten Bruch
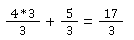
Und dann den Rest
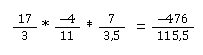
4. Fazit: Brüche dividieren ist einfach, wenn gewusst wie
Wir hoffen, du kannst nach diesem Artikel Brüche sicher dividieren. Wenn du alles von Grundauf noch einmal durchgehen möchtest, dann lese hier alles über die Grundlagen von Bruchrechnung. 🤓
Falls du Hilfe beim Bruchrechnen benötigst, dann ist Nachhilfe vielleicht das Richtige für dich. Teste unsere Mathe-Nachhilfe und vereinbare eine gratis Probestunde mit GoStudent.
Du schaffst das!