Sommaire
- Rappels de cours du théorème de Pythagore
- Exercices sur le théorème de Pythagore
- Corrections des exercices
En 4ème et en 3ème, les élèves apprendront le théorème de Pythagore et devront savoir l’utiliser. Le théorème de Pythagore 📐 est une notion qui tombe systématiquement au brevet. 🎓 Si l’élève apprend la méthode et l’applique en effectuant des exercices, et qu’il prend le temps de se corriger pour apprendre de ses erreurs ou pour vérifier ses bonnes réponses, il ne pourra alors qu’avoir de bons résultats sur les exercices portant sur le théorème de Pythagore. Je vous présente donc le tuto pour réussir tous les exercices ! Il comprend un rappel de cours, des exercices à effectuer, et leurs corrigés.
Lire aussi : Comment préparer son brevet de maths en 5 étapes ? 🎓
1 - Rappels de cours théorème de Pythagore
On commence donc par un petit rappel sur le théorème de Pythagore, sa réciproque, et sa contraposée. 🤗
#1 Le Théorème de Pythagore
📐 Si un triangle est rectangle, alors le carré de son hypoténuse est égal à la somme des carrés des deux autres côtés.
Exemple : Soit ABC un triangle rectangle.
On sait que ABC est un triangle rectangle en A.
D’après le théorème de Pythagore,
On a BC² = AB² + AC².
#2 La Réciproque du Théorème de Pythagore
📐 Si, dans un triangle, le carré du plus grand côté est égal à la somme des carrés des deux autres côtés, alors le triangle est rectangle.
Exemple : Soit ABC un triangle tel que AB = 5, BC = 3 et AC = 4.
AB² = 5² = 25 et BC² + AC² = 3² + 4² = 25
On sait que dans le triangle ABC, le plus grand côté est [AB] et que AB² = BC² + AC².
D’après la réciproque du théorème de Pythagore,
On conclut que ABC est rectangle en C.
#3 La Contraposée du Théorème de Pythagore
📐 Si, dans un triangle, le carré du plus grand côté n’est pas égal à la somme des carrés des deux autres côtés, alors le triangle n’est pas rectangle.
Exemple : Soit ABC un triangle tel que AB = 6, BC = 3 et AC = 4.
AB² = 6² = 36 et BC² + AC² = 3² + 4² = 25
On sait que dans le triangle ABC, le plus grand côté est AB et que AB² ≠ BC² + AC².
D’après la contraposée du théorème de Pythagore,
On conclut que ABC n’est pas rectangle en C.
Lire aussi : Tout savoir sur les programmes de maths au collège
2 - Exercices théorème de Pythagore
Et maintenant, entraînes-toi en effectuant ces exercices ! 💪
Exercice 1
Chacun des triangles ci-dessous est rectangle, trouver la longueur manquante.
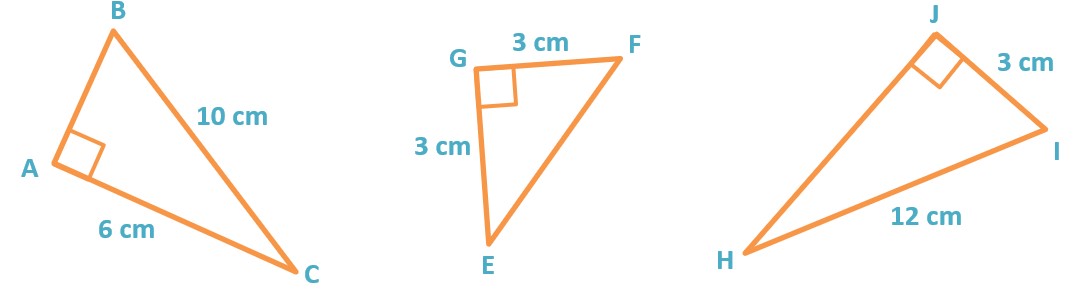
Exercice 2
Pour chaque triangle, démontrer s’il est rectangle ou non.
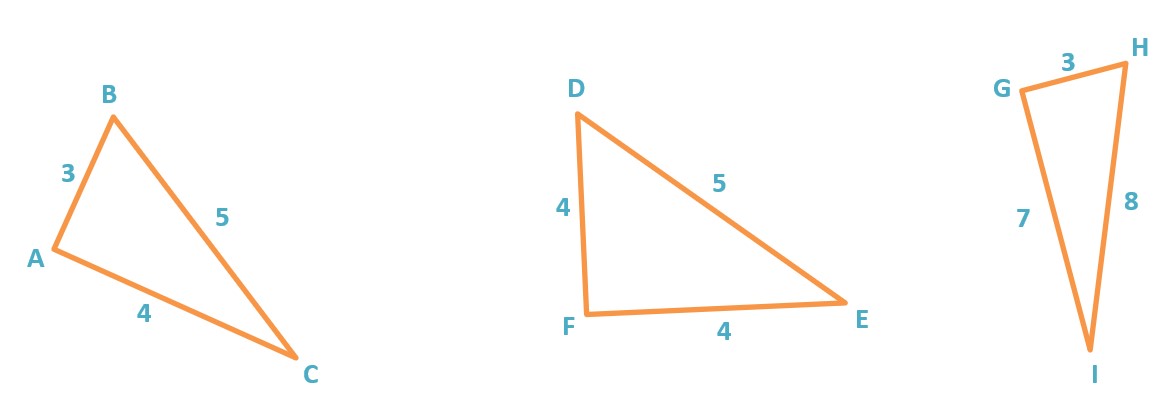Lire aussi : Top 3 des méthodes pour réussir en maths
3 - Corrections des exercices
Après avoir réfléchi et travaillé sur un exercice, il est temps de se corriger ! 🧐
Exercice 1
Chacun des triangles ci-dessous est rectangle, trouver la longueur manquante.
On sait que le triangle ABC est rectangle en A.
D’après le théorème de Pythagore,
On a :
BC² = AC² + AB²
6² + AB² = 10²
36 + AB² = 100
AB² = 100 – 36
AB² = 64
AB = √64
AB = 8 cm
On sait que le triangle EFG est rectangle en G.
D’après le théorème de Pythagore,
On a :
FE² = EG² + GF²
FE² = 3² + 3²
FE² = 18
FE = √18
FE = 4,24 cm
On sait que le triangle IJH est rectangle en J.
D’après le théorème de Pythagore,
On a :
HI² = JI² + HJ²
12² = 3² + HJ²
144 = 9 + HJ²
HJ² = 144 – 9
HJ² = 135
HJ = √135
HJ = 11,62 cm
Exercice 2
Pour chaque triangle, démontrer s’il est rectangle ou non.
On sait que, dans le triangle ABC, [BC] est le plus grand côté.
BC² = 5² = 25
AC² + AB² = 4² + 3² = 16 + 9 = 25
On a BC² = AC² + AB²,
D’après la réciproque du théorème de Pythagore,
On conclut que ABC est rectangle en A.
On sait que, dans le triangle EDF, [DE] est le plus grand côté.
DE² = 5² = 25
DF² + EF² =4² + 4² = 16 + 16 = 32
On a DE² ≠ DF² + EF²,
D’après la contraposée du théorème de Pythagore,
On conclut que ABC n’est pas un triangle rectangle.
On sait que, dans le triangle GHI, [HI] est le plus grand côté.
HI² = 8² =64
GH² + GI² = 3² + 7² = 9 + 49 = 58
On a HI² ≠ GH² + GI²,
D’après la contraposée du théorème de Pythagore,
On conclut que GHI n’est pas un triangle rectangle.
Autre entraînement pour le brevet : Exercices type brevet sur les Volumes.
Et voilà pour ce tuto sur le théorème de Pythagore ! 😁 Si tu as encore des difficultés à intégrer la méthode, ou si d’autres notions te posent problème, n’hésite pas à contacter nos professeurs particuliers certifiés 👨🏼🎓 pour t’aider ! 🎓
