Sommaire
- Rappels sur les fonctions
- Lire graphiquement les images et les antécédents d'une fonction
- Les fonctions affines
- Les fonctions linéaires
- Exercices d’entraînement
Vous vous demandez parfois “pourquoi a-t-on inventé les maths” ? Sachez que les graphiques et les fonctions sont des notions utiles dans tous les domaines. Nous les retrouvons dans le commerce, dans les études sociales, en histoire/géographie… Les graphiques et les fonctions sont omniprésents. C’est pourquoi il est important de les maîtriser. Aujourd’hui, nous allons reprendre ces notions. Dans un premier temps, nous définirons ce qu’est une fonction. Nous allons ensuite apprendre à étudier la représentation graphique d’une fonction. Enfin, nous nous intéresserons aux fonctions affines et linéaires. Après tout cela, tu pourras si tu le souhaites réaliser les exercices d’entraînement pour vérifier tes acquis.
1 - Rappels sur les fonctions
Soit D une partie de l’ensemble des nombres réels R.
Une fonction f définie sur D associe à tout nombre réel x de D un unique nombre réel, noté f(x).
D est appelé l’ensemble de définition de la fonction f.
Nous pouvons donc assimiler une fonction à un algorithme, qui transforme notre nombre initial x (appelé antécédent) en un nouveau nombre f(x) (appelé image).
Une fonction se note comme suit :
f : D → R
x ↦ f(x)
La fonction f définie sur D, qui associe à x le nombre f(x).
Exemple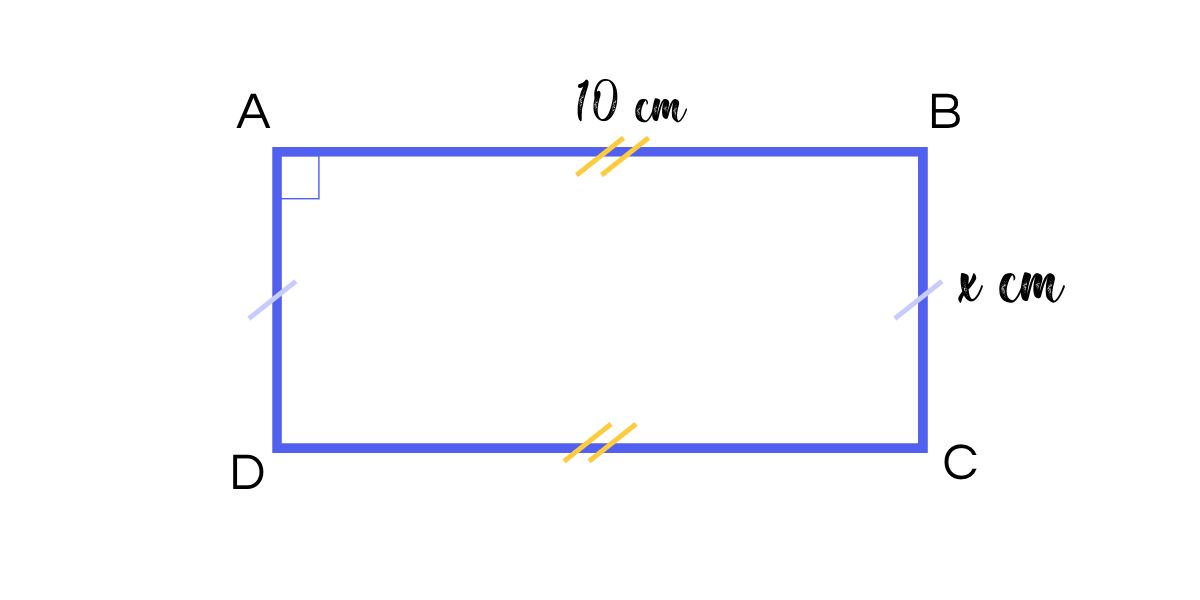
Voici un croquis du rectangle ABCD.
Sa longueur est de 10 cm et sa largeur est de x cm.
Nous pouvons créer une fonction f qui associe à x (l’antécédent) le périmètre de notre rectangle (l’image).
On obtient alors :
f : ] 0 ; 10 ] → R
x ↦ 2(x+10)
Prenons une largeur de 5 cm.
Nous posons alors x = 5, et nous avons alors f(5) = 2×(5+10) = 2×15 = 30.
Le périmètre a donc une longueur de 30 cm.
5 est l’antécédent de 30 par f ; et 30 est l’image de 5 par f.
2 - Lire graphiquement les images et les antécédents d'une fonction
Nous pouvons représenter graphiquement une fonction.
La courbe d’équation y = f(x) est l’ensemble des points du plan dont les coordonnées (x ; y) vérifient y = f(x).
En d’autres termes, chaque point de notre courbe a pour coordonnées (x ; f(x)). Nous lisons donc les antécédents sur l’axe des abscisses et les images sur l’axe des ordonnées.
Exemple : f(x) = 2x + 3 définie sur R
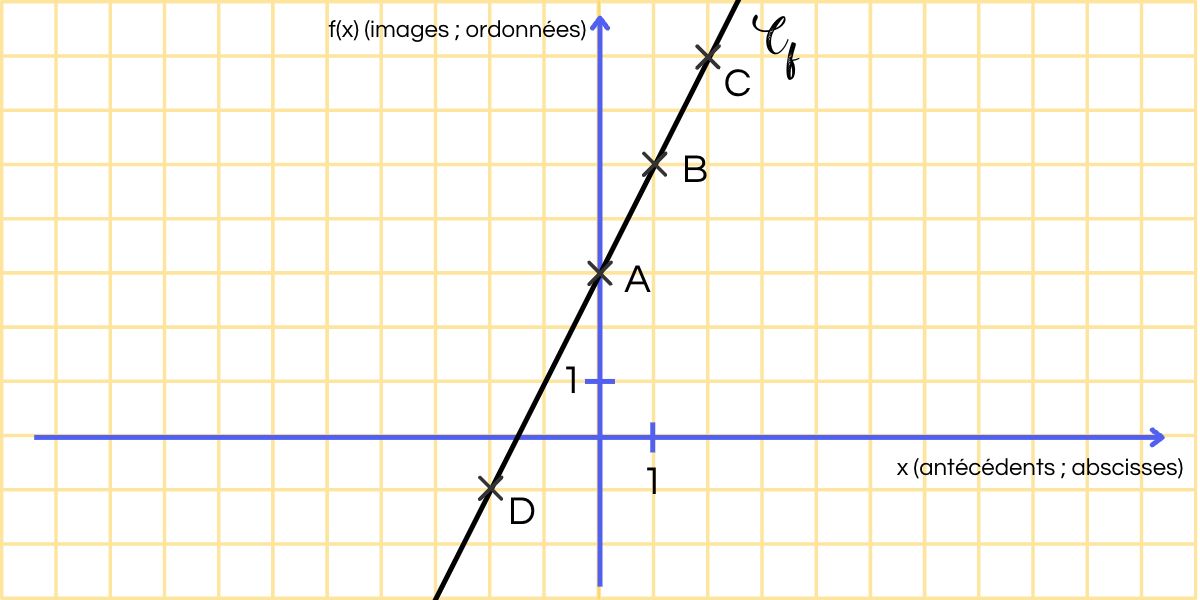
Nous pouvons lire graphiquement les coordonnées de A, B, C et D :
A(0 ; 3) B(1 ; 5) C(2 ; 7) D(-2 ; -1)
On déuit alors graphiquement que :
f(0) = 3
- Autrement dit 3 est l’image de 0 par la fonction f, ou encore 0 est un antécédent de 3 par la fonction f.
f(1) = 5
- Autrement dit 5 est l’image de 1 par la fonction f, ou encore 1 est un antécédent de 5 par la fonction f.
f(2) = 7
- Autrement dit 7 est l’image de 2 par la fonction f, ou encore 2 est un antécédent de 7 par la fonction f.
f(-2) = -1
- Autrement dit -1 est l’image de -2 par la fonction f, ou encore -2 est un antécédent de -1 par la fonction f.
À lire aussi : Top 3 des méthodes pour réussir en maths
3 - Les fonctions affines
Une fonction affine est une fonction du type :
f : ] 0 ; 10 ] → R
x ↦ ax + b
On appelle a le coefficient directeur et b l’ordonnée à l’origine.
Sa courbe représentative est une droite.
- La direction de cette droite dépend de a, si je me positionne sur un point de ma droite et que j’avance de 1 sur les abscisses, alors je me déplace de a sur les ordonnées pour rejoindre la droite. Si a est positif, la droite « monte », s’il est négatif, la droite « descend ».
- Pour calculer a, il me faut connaitre deux points (x, f(x)) et (y, f(y)) et appliquer cette formule :
a = (f(x) - f(y)) / (x - y)
- La « hauteur » de cette droite dépend de b, si je me positionne en (0 ; 0), alors je me déplace de b sur les ordonnées pour rejoindre ma droite. Autrement dit, b = f(0).
- Pour calculer b, il me faut connaître a, et un point (x, f(x)), puis je résous l’équation suivante en remplaçant f(x), x et a par les valeurs connues :
f(x) = ax + b
Exemple 1 : f(x) = 2x + 3 définie sur R
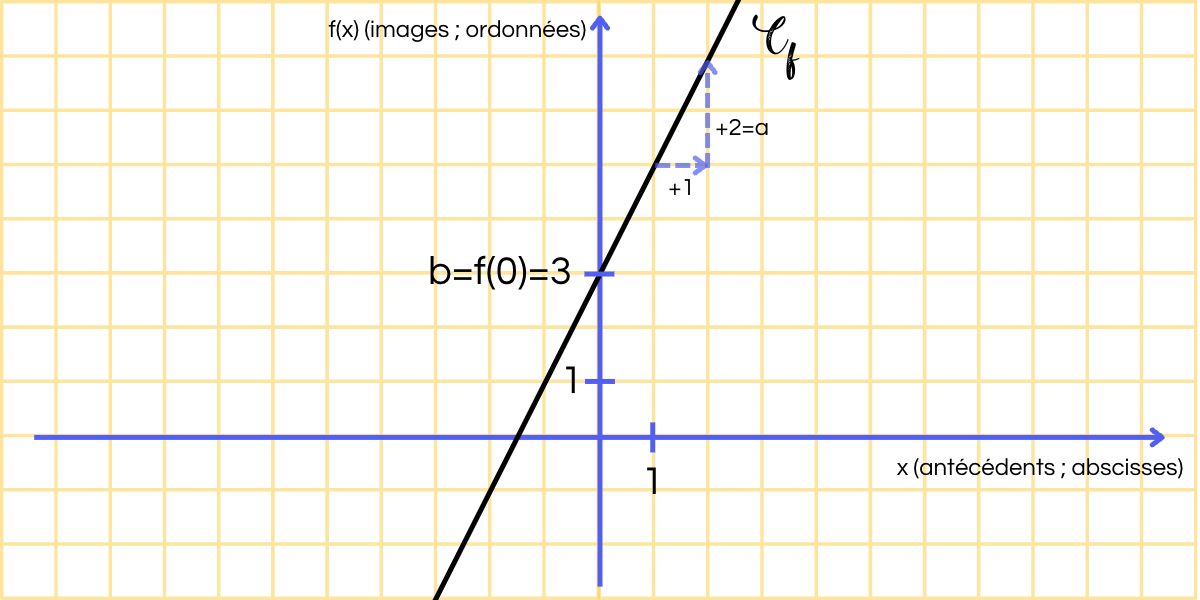
Si je me positionne en A et que j’avance de 1, je monte alors de 2 pour atteindre de nouveau la droite. Comme je monte, le coefficient directeur est positif, donc a = +2.
Si je me positionne en (0 ; 0), je monte de 3 pour atteindre la droite. Comme je monte, l’ordonné est positive, et donc b = +3. Cela revient plus simplement à lire graphiquement l’image de 0.
Exemple 2 : Soit une fonction affine f. On sait que f(2) = 5 et f(5) = 11. Trouver l’expression de f.
f est une fonction affine, donc elle est sous la forme ax + b.
a = (f(2)-f(5)) / (2-5) = (5-11) / (2-5) = (-6) / (-3) = 2
f est donc sous la forme 2x + b. Comme f(2) = 5, on a :
f(2) = 2×2 + b
5 = 4 + b
b = 1
f est donc sous la forme 2x + 1.
f : ] 0 ; 10 ] → R
x ↦ 2x + 1
4 - Les fonctions linéaires
Les fonctions linéaires sont un cas particulier des fonctions affines. C’est une fonction affine dont l’ordonnée à l’origine est nulle. Sa courbe est donc une droite linéaire (une droite qui passe par (0,0)).
Une fonction linéaire est donc une fonction du type :
f : ] 0 ; 10 ] → R
x ↦ ax
Exemple : f(x) = 3x définie sur R
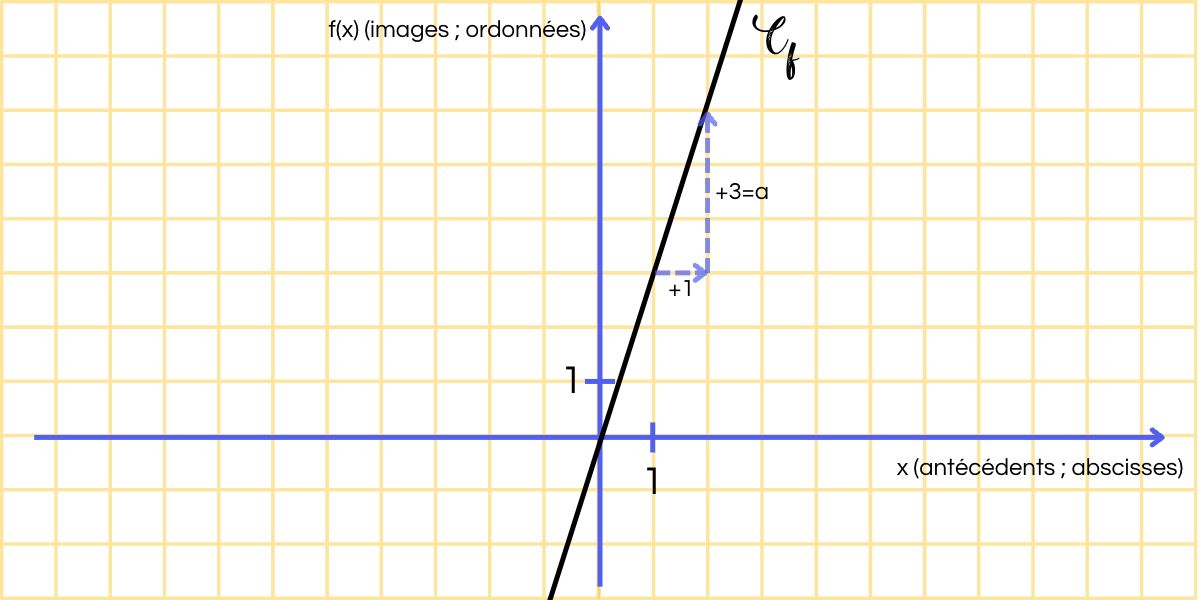
5 - Exercices d’entraînement
Énoncé
Exercice 1
On considère la fonction g dont on donne la courbe représentative Cg ci-dessous.
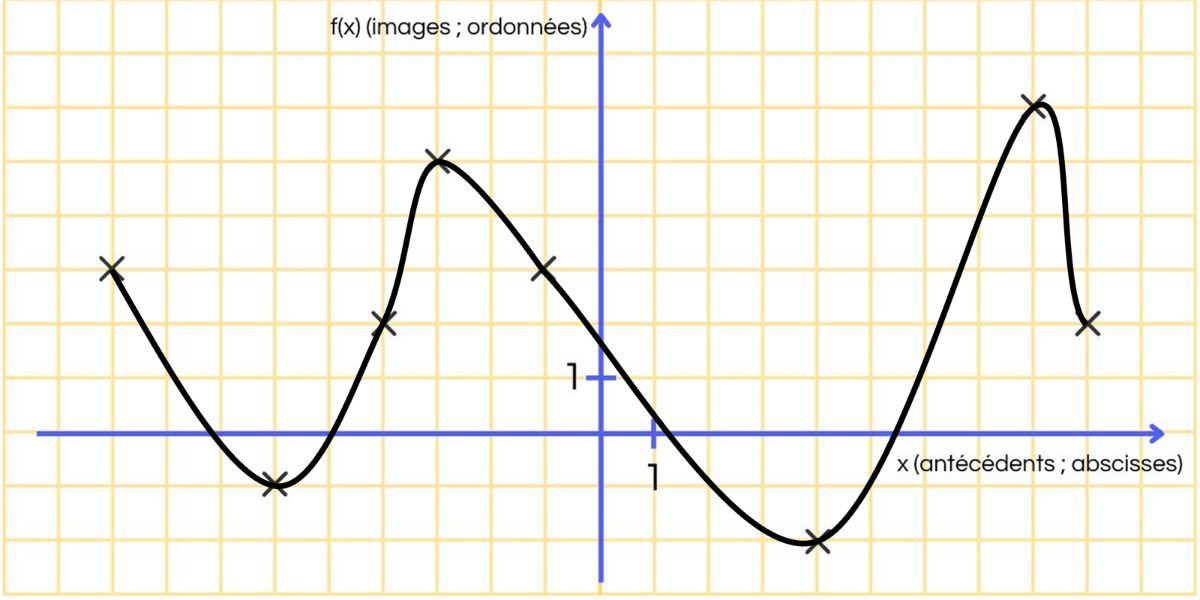
- Quel est l’ensemble de définition Dg de la fonction g ?
- Quel est l’image de -4 par la fonction g ? Et celle de 4 ?
- Quels sont les antécédents par g de -1 ?
- Quel est le maximum de g sur Dg ? Pour quelle(s) valeur(s) est-il atteint ?
Exercice 2
Une usine fabriquer des cartes graphiques pour ordinateur.
On appelle f la fonction qui, a une quantité x de cartes fabriquées associe le coût de fabrication en euros.
On donne ci-après la représentation graphique de f, pour x appartenant à [0 ; 130].
- Lire graphiquement l'image de 30 et interpréter concrètement le résultat.
- Déterminer graphiquement les antécédents éventuels de 600 par la fonction f.
Exercice 3
Soit une fonction affine f définie sur R, telle que (1 ; -1) et (-1 ; -5) appartiennent à sa représentation graphique.
Donner l’expression de la fonction f.
Corrigé
Exercice 1
On considère la fonction g dont on donne la courbe représentative Cg ci-dessous.
- Quel est l’ensemble de définition Dg de la fonction g ?
La fonction g est définie sur [-9 ; 9].
2. Quel est l’image de -4 par la fonction g ? Et celle de 4 ?L’image de -4 par la fonction g est 2.
L’image de 4 par la fonction g est -2.
3. Quels sont les antécédents par g de -1 ?
Les antécédents de -1 par la fonction g sont -6, 2, et 5.
4. Quel est le maximum de g sur Dg ? Pour quelle(s) valeur(s) est-il atteint ?
Le maximum de la fonction g est 6, il est atteint en 8.
Exercice 2
Une usine fabriquer des cartes graphiques pour ordinateur.
On appelle f la fonction qui, a une quantité x de cartes fabriquées associe le coût de fabrication en euros.
On donne ci-après la représentation graphique de f, pour x appartenant à [0 ; 130].
- Lire graphiquement l'image de 30 et interpréter concrètement le résultat.
L’image de 30 par la fonction f est environ 680. Cela veut dire que pour 30 cartes graphiques fabriquées, le coût de fabrication revient à environ 680€.
2. Déterminer graphiquement les antécédents éventuels de 600 par la fonction f.
Les antécédents de 600 par la fonction f sont 0 et environ 55.
Exercice 3
Soit une fonction affine f définie sur R, telle que (1 ; -1) et (-1 ; -5) appartiennent à sa représentation graphique.
Donner l’expression de la fonction f.
Nous savons que f est une fonction affine.
Or, l’expression d’une fonction affine est du type ax + b.
Donc f(x) = ax + b.
Maintenant il nous faut trouver les valeurs de a et b.
On appelle a le coefficient directeur. Pour le trouver, nous pouvons utiliser la formule :
a = (f(x) - f(y)) / (x - y)
Posons x = 1 et y = -1, d’après l’énoncé, f(1) = -1 et f(-1) = -5.
On peut donc calculer a.
a = (-1 – (-5)) / (1 – (-1))
a = (-1 + 5) / (1 + 1)
a = 4 / 2
a = 2
On sait désormais que f(x) = 2x + b.
Maintenant il nous faut trouver b.
On sait que f(1) = -1 et que f(x) = 2x + b.
Si on pose x = 1, on a f(1) = 2 x 1 + b.
Comme f(1) = -1, on obtient l’équation 2 x 1 + b = -1.
Nous n’avons plus qu’à résoudre notre équation pour trouver b.
2 x 1 + b = -1
2 + b = -1
b = -1 - 2
b = -3
On conclut que f(x) = 2x + b.
À lire aussi : Tout savoir sur les programmes de maths au lycée
Nous espérons que cela t’aura aidé à mieux comprendre les représentations graphiques des fonctions, ainsi que les notions de fonctions affines et linéaires.
