Sommaire

1. La géométrie, c'est quoi ?
2. Pourquoi la géométrie est-elle importante ?
3. Où peut-on trouver des formes géométriques dans la nature ?
4. Les formes géométriques 2D les plus importantes
5. C'est quoi la différence entre les parallélogrammes et les quadrilatères ?
6. Et les différents triangles ?
7. Les formes géométriques 3D les plus importantes
8. Fun facts sur les formes géométriques

Cubes, cuboïdes, prismes, pyramides - c'est quoi, tous ces mots à rallonge ? 🤯

Dans cette  introduction, nous allons nous pencher sur la géométrie et tenter de comprendre un peu mieux comment cette branche des mathématiques fonctionne. Nous t'avons concocté des fiches pratiques à télécharger gratuitement pour t'aider à démêler les formes 2D et 3D et à s'assurer que tu ne confondes plus jamais parallélogrammes et pentagones ! 💡

1 - La géométrie, c'est quoi ?

La géométrie, c'est une branche des mathématiques qui se concentre sur les formes et leurs propriétés.💠

Nous allons nous pencher à la fois sur les formes 2D (les formes plates) et sur les formes 3D (les formes qui ont une hauteur, une largeur et une profondeur). Et en un rien de temps, tu sauras reconnaître n'importe quel cylindre ou trapèze !

Ce qui est génial avec la géométrie, c'est que, contrairement à d'autres branches beaucoup plus abstraites des mathématiques, nous pouvons souvent voir des exemples géométriques dans notre vie quotidienne.🍦 

Ce n'est pas une histoire de chiffres, mais de formes réelles et solides qu'on peut observer autour de nous. Nous sommes certains qu'en levant les yeux de cet article et en regardant autour de toi, tu pourras reconnaître au moins 3 formes différentes. C'est ça, la géométrie !

2 - Pourquoi la géométrie est-elle importante ?

La géométrie a énormément d'applications dans la vie réelle, ce qui fait d'elle une matière importante à maîtriser. La géométrie est également directement liée à d'autres domaines des mathématiques tels que la trigonométrie et l'algèbre. Posséder des connaissances solides en géométrie est donc extrêmement important pour s'en sortir en mathématiques.

Quelles sont les utilisations de la géométrie ?

La géométrie est partout, que ce soit dans la nature ou dans le monde créé par les hommes.

• Les formes géométriques sont essentielles à la création de mondes immersifs dans les jeux vidéo. 🎮 
• Les architectes utilisent également la géométrie, puisque construire un bâtiment, ça se résume à emboîter des formes 3D ! 🏛️
• L'art, c'est aussi de la géométrie ! Hé oui, les peintures ne sont qu'une association de formes... et la sculpture, ce sont des formes 3D associées les unes aux autres. 🖼️ 

Tu veux t'entraîner à la maison ? Clique sur le bouton ci-dessous et télécharge notre pense-bête géométrique gratuit !

3 - Où peut-on trouver des formes géométriques dans la nature ?

Même dans la nature, il existe des formes géométriques parfaites ! Il suffit de prendre le temps d'observer un peu.

• Prenez, par exemple, les cellules hexagonales à l'intérieur d'une ruche. 🐝
• La Terre, elle, est une sphère. 🌍
• Les pommes de pin ? Ce sont des cônes ! 🍙

4 - Les formes géométriques 2D les plus importantes

Tu en connais probablement déjà un rayon, mais voici un petit résumé pour te rafraîchir la mémoire :

• Rectangle : Quatre côtés droits et quatre angles droits, les côtés opposés ont la même longueur et deux des côtés qui se font face sont plus longs que les deux autres côtés.
• Carré : Quatre côtés droits et quatre angles droits, tous les côtés ont la même longueur.
• Quadrilatère : Quatre côtés Les rectangles, les carrés, les losanges et les trapèzes sont tous des quadrilatères !
• Triangles : Trois côtés droits et trois angles (nous reviendrons sur les types de triangles plus bas dans l'article).
• Trapèze : Quatre côtés droits et une paire de côtés parallèles.
• Parallélogramme : Un type de quadrilatère avec deux paires de côtés parallèles et aucun angle droit.
• Losange : Un type de parallélogramme avec quatre côtés (non droits) et quatre angles (non droits), les côtés opposés étant égaux et les angles opposés étant égaux. Les diagonales se coupent mutuellement à angle droit.
• Pentagone : Cinq côtés et cinq angles égaux.
• Hexagone : Six côtés et six angles égaux.
• Octogone : Huit côtés et huit angles égaux.

5 - C'est quoi la différence entre les parallélogrammes et les quadrilatères ?

Tous les parallélogrammes sont des quadrilatères, mais tous les quadrilatères ne sont pas forcément des parallélogrammes ! Un quadrilatère, c'est n'importe quelle forme dotée de quatre côtés. Un parallélogramme, c'est un peu plus compliqué : cette forme contient également quatre côtés, mais elle n'a aucun angle droit et deux de ses côtés sont parallèles.

6 - Et les différents triangles ?

Les triangles sont un sujet de recherche plus approfondie dans une autre branche des mathématiques, la trigonométrie, mais ils ont également leur importance en géométrie. 

Voici donc un petit rappel sur les triangles.

• Triangle isocèle : triangle dont au moins deux côtés sont égaux.

• Triangle équilatéral : Les trois côtés ont la même longueur (en latin, "equi" signifie égal).

• Triangle scalène :  Les côtés sont inégaux, aucun des angles n'est égal.

• Triangle aigu :  Tous les angles mesurent moins de 90°.

• Triangle à angle droit : Un angle mesure 90°.

• Triangle obtus : Un des angles mesure plus de 90°.

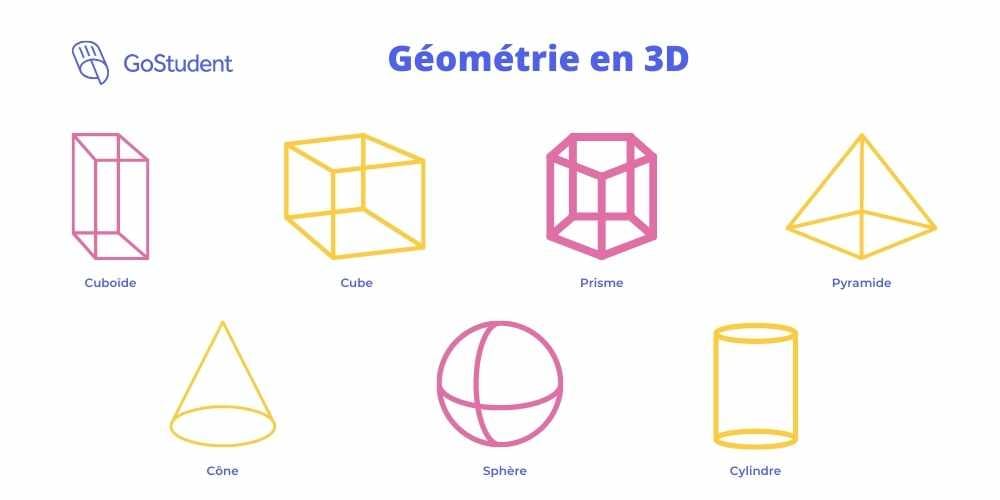
7 - Les formes géométriques 3D les plus importantes

• Parallélépipède - Six faces rectangulaires dont tous les angles sont droits.
• Cube : Six faces carrées égales dont tous les angles sont droits.
• Prisme : Deux formes identiques se faisant face, les autres faces étant des quadrilatères. 
• Pyramide : Forme à base carrée ou triangulaire tous les autres côtés sont des triangles qui se rencontrent en un point.
• Cône : Forme à base circulaire avec des côtés arrondis qui se rencontrent en un point.
• Sphère : Une face arrondie, comme une balle (ou la Terre). 
• Cylindre : Deux faces circulaires parallèles et une forme rectangulaire arrondie entre ces deux faces circulaires. 

8 - Fun facts sur les formes géométriques

• Euclide, un mathématicien de la Grèce Antique, est considéré comme le père de la géométrie. Cela dit, il est difficile de savoir exactement qui a découvert la géométrie, car il est très probable que les travaux d'Euclide se soient fondés sur d'autres écrits qui se sont perdus à travers l'Histoire.
• En général, on part du principe que la géométrie a été découverte dans le but d'aider à la construction de bâtiments et de comprendre l'astronomie.
• La géométrie et l'algèbre sont deux branches très courantes des mathématiques, mais il est dit que la géométrie a été développée plus de 1000 ans après l'algèbre.

Lire aussi : Pourquoi a-t-on inventé les maths ?

La géométrie, ce n'est pas ton truc ? Pourquoi ne pas essayer une leçon gratuite avec un de nos professeurs particuliers en mathématiques qui peut t'aider à y voir plus clair ?