Todas las figuras geométricas explicadas de forma sencilla

Capítulos:

1. ¿Qué son las figuras geométricas? Una explicación sencilla
   
2. Geometría 2D: Las figuras geométricas planas o bidimensionales
3. Geometría 3D: Las figuras geométricas tridimensionales o con volumen
   
   

La geometría es esa parte de las matemáticas que se encarga de describir todas las formas y figuras que vemos en el espacio, desde simples cuadrados hasta figuras mucho más complejas. Estas figuras geométricas pueden ser algo difíciles de entender al principio pero, después de leer este artículo te darás cuenta de que son mucho más sencillas de lo que parecen. 😀

¿Qué son las figuras geométricas? Una explicación sencilla

Las figuras geométricas han tenido muchas definiciones con el paso de los siglos siendo, a día de hoy, definidas como superficies planas delimitadas por líneas que pueden ser rectas o curvas. No te eches las manos a la cabeza si te ha parecido una definición un poco complicada, 😱 porque es mucho más simple de lo que parece. 

Cualquier objeto que veas ahora mismo es, más o menos, una figura geométrica. Por ejemplo, la televisión sería un rectángulo 📺 y la mesa un cuadrado. Es decir, todas ellas están limitadas. Es importante entender y conocer bien las figuras geométricas porque, más allá de servir para aprobar matemáticas, forman parte de nuestra vida, todo nuestro entorno está rodeado de figuras geométricas con nombre: círculo, cuadrado, rectángulo, triángulo. 

Geometría 2D: Las figuras geométricas planas o bidimensionales

En primer lugar,  vamos a empezar por lo más sencillo, que son las figuras bidimensionales, 2D o en dos dimensiones. Como su propio nombre indica, estas son figuras planas con dos dimensiones: largo y ancho. Es decir, no tienen volumen ni profundidad. Estas figuras geométricas se construyen con la unión de varios puntos. De ahí que sean las más simples. A continuación vamos a desgranar los elementos más simples de la geometría bidimensional. 

Punto

A pesar de que es el elemento geométrico más sencillo, es probablemente el más difícil de explicar, ya que no tiene representación física. 🤔 Un punto es una figura geométrica sin dimensión, ni volumen ni longitud y representa una localización en un plano, la cual viene dada por unas coordenadas. Un punto describe una posición en el plano, la cual se describe con sus respectivas coordenadas del eje X y del eje Y. 

Línea

La línea es una figura geométrica mucho más fácil de entender, porque no es más que una sucesión de puntos y, por tanto, esta ya tiene dimensión y se puede visualizar. 📉 Una línea recta puede ser de varios tipos, atendiendo a si están acotadas o no. Es decir, si son líneas infinitas en ambas direcciones o si, por el contrario, tienen un punto inicial, un punto final o ambos. 

Una vez que conocemos los dos elementos fundamentales de la geometría, podemos empezar a hablar de las diferentes figuras geométricas básicas. 

Triángulo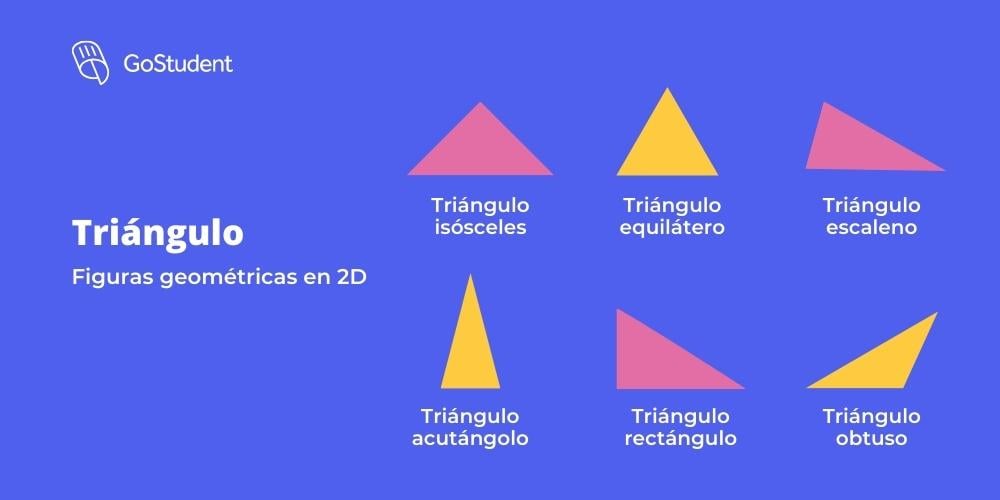

Se considera la más básica porque es la que menos lados tiene (a excepción del círculo que veremos más adelante). Si unimos tres puntos entre sí formamos un triángulo. 📐 La figura formada cuenta con tres lados y tres ángulos, como su propio nombre indica. Los lados se nombran con A, B y C mientras que los ángulos se nombran con sus equivalentes en el alfabeto griego: α, β y γ. 

Es muy interesante que un triángulo sea equivalente a dividir un cuadrado por la mitad (cortando por los vértices opuestos), porque esto nos permitirá calcular su área de manera sencilla. El área de las figuras geométricas es uno de los datos más importantes y necesarios en geometría. 

Área del triángulo = (base * altura) /2  

Siendo la altura la distancia entre un vértice y el centro de su lado opuesto. 

Perímetro del triángulo = A + B +C 

Existen diferentes tipos de triángulos atendiendo a la longitud de sus lados y a sus ángulos: 

Atendiendo a sus lados:

• Equilátero: todos sus lados son iguales. 
• Isósceles: tiene dos lados iguales y uno desigual. 
• Escaleno: todos sus lados son de diferente longitud. 
  
  

Atendiendo a sus ángulos: 

• Agudo: todos sus ángulos son menores de 90º.
• Recto: tiene un ángulo exactamente de 90º.
• Obtuso: cuenta con ángulo de más de 90º. 

Cuadriláteros

El rectángulo es la siguiente figura geométrica importante y es que esta cuenta con 4 lados y, por ello, con cuatro ángulos. El cuadrado no es más que un tipo de rectángulo en el que los 4 lados tienen las mismas medidas. Los ángulos, tanto del cuadrado como del rectángulo, son siempre de 90º .

• Área del rectángulo = base x altura
• Área del cuadrado = lado x lado
• Perímetro del rectángulo = 2 x base + 2 x altura 
• Perímetro del cuadrado = 4 x lado
  
  

Un trapezoide es un tipo de cuadrilátero, puesto que cuenta con cuatro lados, sin embargo, no es un rectángulo, porque sus ángulos no son rectos. Cuenta con dos lados paralelos, de manera que un trapezoide podría dividirse en dos triángulos y un rectángulo. brain

Área del trapezoide = ½ (A + C) * h 

Siendo “A” y “C” los lados opuestos y “h” la altura. 

Perímetro del trapezoide = A +B + C + D

Dentro de los trapezoides podemos diferenciar varios tipos: 

• Trapezoide isósceles: los lados no paralelos entre sí tienen la misma longitud. 
• Trapecio rectángulo: uno de los lados es perpendicular a los dos lados paralelos. 
• Paralelogramo: aquel trapezoide que tiene sus lados opuestos paralelos, es decir, el cuadrado y el rectángulo son paralelogramos especiales. 
• Rombo: tiene los cuatro lados de la misma longitud pero, a diferencia del cuadrado, sus ángulos no son rectos. 
  
  

Polígono

Las figuras geométricas que tienen más de 4 lados se denominan polígonos. Existen tantos polígonos como puedas imaginar, eso sí, hacer dibujos de estas figuras geométricas no será tan fácil, sobre todo, si quieres hacer uno con muchísimos lados. Los polígonos más conocidos son: 

• Pentágono: polígono de 5 lados. 
• Hexágono: polígono de 6 lados. 
• Octágono: polígono de 8 lados. 
  
  

Círculo

Sin duda una de las figuras geométricas más curiosas. Si te paras a pensar en la forma de un círculo, 🧠 este está formado por una sola línea, cuyo inicio y su final se unen en un mismo punto. Presenta un diámetro que es igual a dos veces su radio y, por tanto, se trata de una figura simétrica. 

Área del círculo = 𝛑 * r2

Perímetro del círculo = 2 *𝛑 * r

Geometría 3D: Las figuras geométricas tridimensionales o con volumen

Ahora vamos un paso más allá y es que las figuras geométricas pueden tener más dimensiones. A parte del largo y el ancho, las figuras pueden tener una profundidad, lo cual les otorga un volumen, que también se puede calcular. 🧮

La geometría de los cuerpos tridimensionales es mucho más compleja, sobre todo si queremos hacer dibujos de estas figuras geométricas, ✏️ debido a que el hecho de que tengan profundidad dificulta el poder plasmarlo en un plano, en un folio. Para que te resulte más sencillo, a continuación se muestran las figuras 3D más importantes y que deberías de conocer.

Cuboide u ortoedro

El cuboide u ortoedro sería la figura geométrica 3D obtenida a partir del rectángulo. 

• Caras: 6
• Vértices: 8 
• Lados: 12
• Superficie = 2 (A*B + A*C + B*C)
• Volumen = A * B * C 

Cubo

Si el cuboide era la figura geométrica 3D procedente de añadir profundidad a un rectángulo, el cubo lo es del cuadrado. 🧊 En este caso todas las caras son iguales entre sí. 

• Caras = 6
• Vértices = 8
• Lados = 12
• Superficie = 6 * A²
• Volumen = A³
  
  

Prisma

Un prisma es una figura geométrica formada por dos bases poligonales, paralelas entre sí y tantas caras rectangulares como lados tenga la base. Con la plantilla en PDF para descargar, que puedes encontrar en este artículo, te resultará mucho más fácil visualizarlo. 🔍 En este caso no podemos hablar de cuantos lados y caras tiene, porque dependerá de qué polígonos constituyan las bases de este. La superficie será la suma de las superficies de cada figura geométrica y el volumen será ese área multiplicado por la longitud del rectángulo que une las bases. 

Pirámide

La pirámide es idéntica a un prisma pero, en lugar de tener dos caras paralelas como bases, solo tiene una, de modo que las caras laterales son triángulos que se unirán en un mismo punto. Calcular el área y el volumen de esta dependerá, al igual que en el caso anterior, del polígono que forma la base.  

Cilíndro

Si has entendido cómo se construye un prisma, entenderás con facilidad que es un cilindro, porque son exactamente iguales pero, en lugar de que las bases sean polígonos con varios lados, son círculos. 🟠 Esto hace que solo haya una cara perpendicular a estas, que es la que une ambos círculos creando una figura geométrica 3D. 

• Caras = 3
• Vértices = 0
• Lados = 2 (las líneas curvas que constituyen los círculos de las bases se consideran lados/bordes)
• Superficie = superficie lateral + 2 * (superficie de base) = 2 * r  (r + h)
• Volumen = r2 * h
  
  
  

Cono

La diferencia entre prisma y pirámide es la misma que existe entre el cilindro y el cono. 🍧 Un cono es como un cilindro pero en lugar de tener dos bases tiene tan solo una, por tanto, la cara lateral confluye en un único punto. 

• Caras = 2 
• Vértices = 1
• Lados  = 1 
• Superficie = superficie lateral + superficie de base = r2 + r * s
• Volumen = 12 * r * h
  
  

Esfera

Una figura geométrica interesante porque, a pesar de ser en 3D, está formada por una sola cara y es que se trata de la figura tridimensional del círculo. ⚽ Se trata de una figura que no tiene vértices ni lados. 

• Caras = 1 
• Vértices = 0
• Lados = 0
• Superficie = 4 * r2
• Volumen = 4/3 * r3
  
  

Lo visto en este artículo es tan solo el principio de todo lo que podrás descubrir si profundizas en el mundo de la geometría. No olvides que aprender también puede ser entretenido. Busca las diferentes figuras geométricas en tu casa y en clase y descubre si eres capaz de reconocerlas en tu día a día. 😁 ¡Estamos seguros de que sí!