Pq-Formel anwenden: Beispiele, Aufgaben, Herleitung & mehr

Kapitel:

1. Die PQ-Formel 
2. Die PQ-Formel mit Beispiel zum Anwenden
3. Nullstellen der Quadratischen Gleichung bestimmen
4. Die PQ-Formel üben mit Aufgaben
5. Der PQ-Formel Song
6. Die Mitternachtsformel (ABC-Formel)
7. Extra: Die Herleitung der PQ-Formel

Quadratische Formeln sehen deutlich schwieriger aus, als sie sind. 😎 Tatsächlich kannst du sie im Handumdrehen lösen. In diesem Artikel erklären wir dir einfach und übersichtlich, wie du Quadratische Gleichungen mit der PQ-Formel auflösen kannst. Zusätzlich findest du weiter unten PQ-Formel Aufgaben und Lösungen. 🤗 Viel Erfolg!

Wenn du ganz von vorne beginnen möchtest, solltest du hier nachlesen, wie man Gleichungen auflösen kann. 🤓

Die pq-Formel

Die PQ-Formel ist eine Standardmethode zur Lösung Quadratischer Gleichungen. Diese sind Gleichungen, deren Variablen (x, y, z etc.) eine erste oder zweite Potenz enthalten (n^1 oder n^2). Wichtig ist, dass es keine dritte oder höhere Potenz in einer Quadratischen Gleichung gibt! Auch muss die Variable x zwingend in der Potenz vorkommen und nicht nur im linearen Glied (3x). So sieht eine Quadratische Gleichung aus:

5x² + 3x = 54

x² = 64

Um eine Quadratische Gleichung mit der PQ-Formel lösen zu können, muss sie immer in die sogenannte normale Form gebracht werden. 🧐 Die meisten Quadratischen Gleichungen sind allerdings in der allgemeinen Form aufgeschrieben, wo der Koeffizient von x²  ungleich 1 ist. Die allgemeine Form sieht so aus:

ax² + bx + c = 0

Die Normalform hingegen sieht so aus - wo der Koeffizient von x² gleich 1 ist. 

x² + px + q = 0

Diese Formen lassen sich meist mit der Äquivalenzumformung erreichen. Darunter versteht man allgemein, dass die Terme auf beiden Seiten der Gleichung so umgestellt werden, dass die Inhalte äquivalent, also gleichwertig, bleiben. Nehmen wir zum Beispiel diese Quadratische Gleichung:

4x² + 2x = 25

Wie können wir daraus die allgemeine Form erreichen? In diesem Beispiel rechnest du einfach -25, das schreibt sich dann so:

4x² + 2x = 25    | -25

-> 4x² + 2x - 25 = 0

Hier entspricht a = 4, b = 2 und c = -25. Die drei Koeffizienten a, b und c haben außerdem die Namen quadratisches Glied, lineares Glied und konstantes Glied. 🔤

Von hier kommst du dann zur Normalform, indem du die Gleichung durch a teilst:

4x² + 2x - 25 = 0   | /4

-> x² + 0,5x - 6,25 = 0

Durch diesen letzten Schritt hast du nun die Normalform erreicht, von der aus du mit der PQ-Formel weitermachen kannst. Diese benutzt die p = 0,5x und q =-6,25.

Die PQ-Formel wird oft mit der Mitternachtsformel 🌠 verwechselt. Die Mitternachtsformel heißt angeblich so, weil sie aufgrund ihrer Einfachheit so wichtig und anwendbar ist, dass Schüler sie auch dann anwenden können sollten, wenn sie mitten in der Nacht geweckt werden. 

Wie nun genau diese PQ-Formel aussieht und wie du sie anwenden kannst, erfährst du im nächsten Teil dieses Artikels. 

Die pq-Formel mit Beispiel zum Anwenden

Die PQ-Formel sieht folgendermaßen aus:

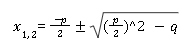
Das ^-Zeichen zeigt die Potenz an. b^2 bedeutet also b². Wie du siehst, kommen nur noch zwei der ursprünglich drei Koeffizienten unserer obigen Gleichung in dieser PQ-Formel vor - das lineare Glied und das konstante Glied.

Diese musst du tatsächlich nur in die Formel einsetzen. Wir haben also:

p = 0,5

q = -6,25

Damit sieht die Formel so aus:

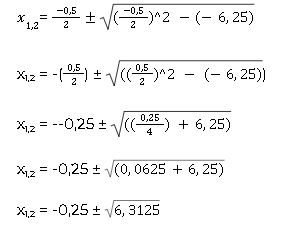
Daraus ergeben sich dann zwei Lösungen:

x₁ = -0,25 + 2,51247 = 2,26247

x₂ = -0,25 - 2,51247 = -2,76247

Das liegt daran, dass es ja ein x₁  und ein x₂ gibt. Die Quadratische Gleichung ist sowohl mit negativen ➖ als auch mit positiven ➕ Vorzeichen wahr. 

Nullstellen der Quadratischen Gleichung bestimmen 

Die Variable x als Unbekannte, 👻 die die quadratische Gleichung löst, ist die Zahl, für die die Gleichung wahr ist. Eine quadratische Gleichung mit reellen Zahlen kann null, einen oder zwei Werte in der Lösungsmenge haben.

Um sich das vorzustellen, solltest du die Gleichung als Parabel verstehen. Sie kann die Achse an zwei Stellen kreuzen oder sie an keinem Punkt berühren. Diese Punkte werden als Nullstellen bezeichnet.

Mithilfe der sogenannten Diskriminante kannst du die Anzahl der Nullstellen zählen. Dies funktioniert wie folgt

D=b² - 4ac

Daraus folgen drei Szenarien:

1. Positive Diskriminante - Es gibt zwei Nullstellen, also zwei Lösungen.
2. Negative Diskriminante - Es gibt keine Nullstelle also keine reelle Zahl, die die Gleichung lösen kann.
3. Diskriminante ist Null - Es gibt eine Nullstelle, also eine doppelte und gleiche Lösung

pq-Formel üben mit Aufgaben

Hier geben wir dir ein paar Beispielaufgaben zum Üben. Wenn du Schwierigkeiten hast, kann dir vielleicht Mathe-Nachhilfe helfen. Vereinbare doch eine kostenlose Probestunde bei GoStudent und teste unsere Online-Nachhilfe gratis.

Übungsaufgaben:

x² + 10x + (-24) = 0

x² + 2x + (-8) = 0

x² + (-10)x + 25 = 0

x² + (-3)x + 2 = 0

x² + (-6)x + 8 = 0

x² + (-6)x + (-7) = 0

(-2)x² + (-2)x + 24 = 0

2x² + 16x + 30 = 0

9x² + 18x + (-72) = 0

-4x² + (-24)x + (-32) = 0

Lösungen:

x² + 10x + (-24) = 0

x₁ = -5 + 7 = 2

x₂ = -5 - 7 = -12

x² + 2x + (-8) = 0

x₁ = -1 + 3 = 2

x₂ = -1 - 3 = -4

x² + (-10)x + 25 = 0

x₁ = 5 + 0 = 5

x₂ = 5 - 0 = 5

x² + (-3)x + 2 = 0

x₁ = 1,5 + 0,5 = 2

x₂ = 1,5 - 0,5 = 1

x² + (-6)x + 8 = 0

x₁ = 3 + 1 = 4

x₂ = 3 - 1 = 2

x² + (-6)x + (-7) = 0

x₁ = 3 + 4 = 7

x₂ = 3 - 4 = -1

(-2)x² + (-2)x + 24 = 0

x₁ = -0,5 + 3,5 = 3

x₂ = -0,5 - 3,5 = -4

2x² + 16x + 30 = 0

x₁ = -4 + 1 = -3

x₂ = -4 - 1 = -5

9x² + 18x + (-72) = 0

x₁ = -1 + 3 = 2

x₂ = -1 - 3 = -4

-4x² + (-24)x + (-32) = 0

x₁ = -3 + 1 = -2

x₂ = -3 - 1 = -4

Der pq-Formel Song

Wusstest du, dass es sogar einen Song zur PQ-Formel gibt? 🎤 Wir finden das natürlich absolut klasse und besonders als Vorbereitung auf die nächste Prüfung! Dieser Song mag vielleicht nicht die Charts stürmen und befindet sich höchstwahrscheinlich auch nicht in deinen Spotify-Listen. Aber wir sind der Meinung, dass er sich trotzdem lohnt. 🤠 Denn er erklärt dir einfach und witzig, wie man die PQ-Formel verwendet. Hier siehst du die erste Strophe:

,,Hast du schon mal versucht eine Gleichung mit Quadraten drin zu lösen?

Wenn ja, dann weißt du sicher dabei darf man nicht dösen

Denn, ob es eine Lösung, keine Lösung, zwei Lösungen gibt

Weiß man oft erst, wenn sich das dann durch eine Rechnung ergibt”

Das ganze Video findest du auf Youtube!

Die Mitternachtsformel (ABC-Formel)

Die Mitternachtsformel ist ebenfalls zur Lösung von Quadratischen Gleichungen geeignet. Allerdings wird sie bei anderen Voraussetzungen verwendet, ist also kein direkter Ersatz für die PQ-Formel. 

Hier reicht die allgemeine Form aus, das bedeutet, du musst die Gleichung nicht zuerst in die Normalform bringen. Nehmen wir einmal das Beispiel von oben:

4x² + 2x = 25    | 25

= 4x² + 2x - 25 = 0

Diese Gleichung kannst du nun mit der Mitternachtsformel lösen. Diese sieht so aus:

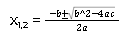
Die Mitternachtsformel heißt ja eigentlich ABC-Formel. Jetzt siehst du auch, warum das so ist. Alle vier Koeffizienten a, b und c kommen hier vor:

a = 4

b = 2

c = -25

 Dementsprechend musst du nur einsetzen. Das sieht dann so aus:

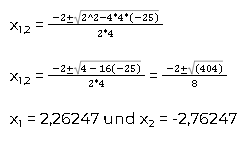
Extra: Die Herleitung der pq-Formel

Du kannst eine quadratische Gleichung nicht einfach nach x lösen. Wenn du die p-q-Formel herleitest, musst du eine quadratische Gleichung nach x mit einem Verfahren lösen. Die Herausforderung bei der p-q-Formel besteht darin, zunächst ein quadratisches Problem in eine Form umzuwandeln, die die Anwendung der ersten binomischen Formel ermöglicht. 🤔

Die PQ-Formel, die du zuvor gelernt hast, wird dann angewendet. Mach dir keine Sorgen! Diese Information musst du gar nicht oder eher für die Vorbereitung auf das Mathe-Abitur können. Frage bei Zweifel bei deinem Lehrer nach! 😅